Chapitre 4 zazou : une nouvelle approche

4.1 Processus d’Ornstein-Uhlenbeck

Un processus d’Ornstein-Uhlenbeck (OU) de force de rappel \(\ou{\alpha}\), de valeur optimale \(\ou{\optim}\), et d’écart-type \(\ou{\sigma} > 0\) est un processus gaussien qui satisfait l’équation différentielle stochastique suivante :

\[\begin{equation*} \dx{W_t} = - \ou{\alpha} (W_t - \ou{\optim}) \dx{t} + \ou{\sigma}\dx{B_t}, \end{equation*}\]

avec \(B\) le mouvement brownien unidimensionnel standard.

Si \(W_0\) est connu et fixé, l’espérance du processus vaut \(\EE{W_t} = W_0 e^{-\ou{\alpha} t} + \ou{\optim}\left(1 - e^{-\ou{\alpha} t}\right)\) et la covariance du processus est donnée par

\[\CC{W_t, W_s} = \frac{\ou{\sigma}^2}{2\ou{\alpha}}\left(e^{-\ou{\alpha} \left|t-s\right|} - e^{-\ou{\alpha} \left(t+s\right)}\right).\]

Le processus est gaussien et il admet pour loi limite \(\normal{\ou{\optim}}{\frac{\ou{\sigma}^2}{2\ou{\alpha}}}\), dont la variance est finie.

De par leurs propriétés, les processus d’Ornstein-Uhlenbeck sont devenus populaires pour modéliser l’évolution de traits biologiques continus, comme la masse corporelle des mammifères (Freckleton, Harvey, & Pagel, 2003).

Il est également possible de faire évoluer un processus d’Ornstein-Uhlenbeck sur un arbre (Bastide, Mariadassou, & Robin, 2017). Le long d’une branche, les paramètres du processus sont fixes. À chaque nœud, une branche se divise (en deux dans le cas d’un arbre binaire) et le processus donne naissance à deux copies indépendantes ayant la même valeur initiale au point de branchement. Cela induit notamment une dépendance statistique entre tous les descendants d’un même ancêtre. Cette dépendance est d’autant plus forte que l’ancêtre est récent. Sur la figure 4.1, le processus vert partant de \(N_1\) jusqu’à \(N_2\) donne naissance à deux processus \(T_4\) et \(T_5\), jaune et bleu, lorsqu’il arrive au nœud \(N_2\).

De plus, à chaque branchement, un changement dans les paramètres du processus est susceptible de se produire. Dans ce cas, le processus garde la même valeur au nœud mais continue sa trajectoire avec les nouveaux paramètres. C’est le cas en \(N_3\) dans la figure 4.1 où le processus orange a subi un changement dans sa valeur optimale \(\ou{\optim}\) par rapport au processus rouge : la trajectoire est continue et le processus dérive vers la nouvelle valeur optimale.

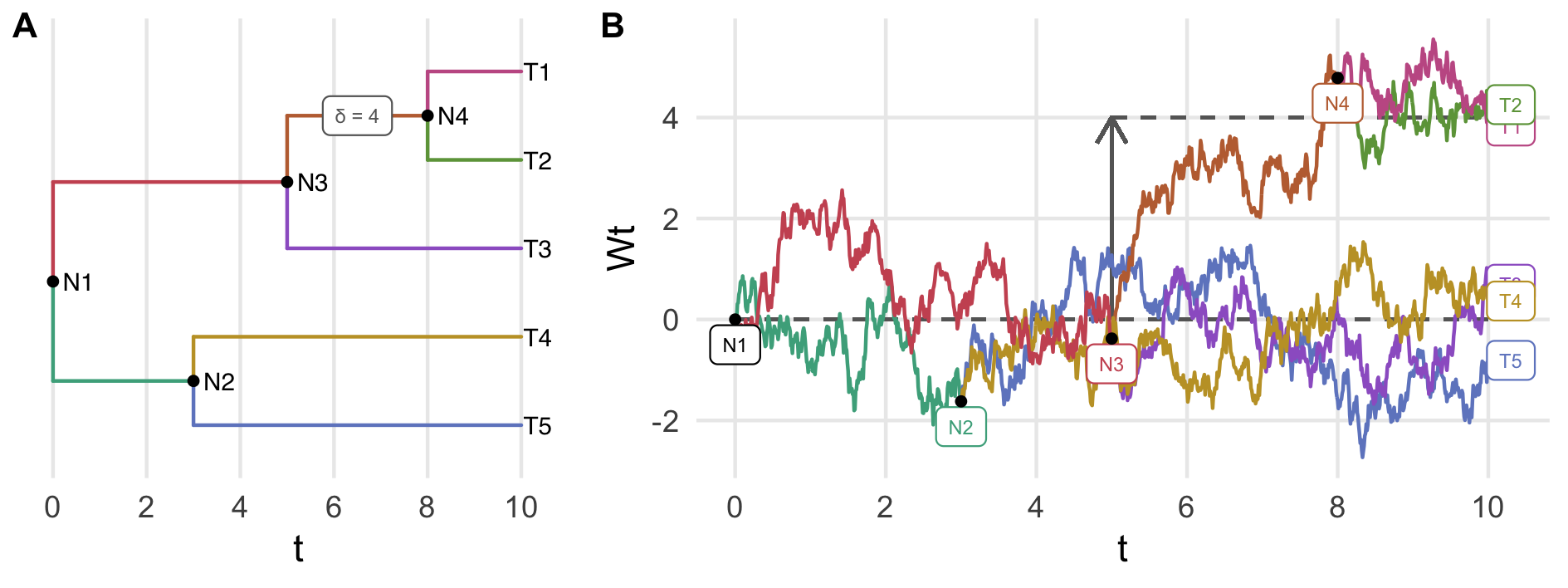
Figure 4.1: Exemple d’un processus d’Ornstein-Uhlenbeck sur un arbre à 5 feuilles. À chaque branchement, le processus se scinde en deux processus indépendants ayant la même valeur initiale. Les paramètres sont conservés sauf lors d’un saut dans la valeur optimale, comme sur la branche conduisant à \(N_4\).

Le produit matriciel de la matrice d’incidence \(T\) par le vecteur de sauts \(\shifts\) permet d’effectuer la somme cumulée des sauts le long des branches pour obtenir la valeur optimale du processus aux feuilles. Dans l’exemple de la figure 4.1,

\[\begin{equation*} \oui{\optim}{\{\text{feuilles}\}} = T \shifts = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 4 \\ \end{bmatrix} = \begin{bmatrix} 4 \\ 4 \\ 0 \\ 0 \\ 0 \\ \end{bmatrix}. \end{equation*}\]

En notant \(\oui{\optim}{i}\) la valeur optimale du processus sur la branche descendant au nœud \(i\), la loi à ce nœud conditionnellement à son parent est

\[\begin{equation*} X_i|X_{\text{pa}(i)} \sim \mathcal{N}\left( X_{\text{pa}(i)} e^{-\ou{\alpha} \ell_i } + \oui{\optim}{i} \left(1-e^{-\ou{\alpha} \ell_i}\right), \frac{\ou{\sigma}^2}{2\ou{\alpha}} \left(1 - e^{-2\ou{\alpha} \ell_i}\right) \right). \end{equation*}\]

Ceci permet d’avoir une expression pour la covariance entre les nœuds \(i\) et \(j\). Dans le cas où \(P = \pa(i)=\pa(j)\), on a

\[\begin{equation*} \begin{aligned} \CC{X_i, X_j} & = \EE{X_iX_j} - \EE{X_i} \EE{X_j} \\ & = \EE{\EE{X_iX_j\mid P}} - \EE{\EE{X_i\mid P}} \EE{\EE{X_j \mid P }} \\ & = \EE{\left(P e^{-\ou{\alpha}\ell_i} + \oui{\optim}{i} \left(1-e^{-\ou{\alpha}\ell_i}\right)\right) \left(P e^{-\ou{\alpha}\ell_j} + \oui{\optim}{j} \left(1-e^{-\ou{\alpha}\ell_j}\right)\right)} \\ & \qquad - \EE{P e^{-\ou{\alpha}\ell_i} + \oui{\optim}{i} \left(1-e^{-\ou{\alpha}\ell_i}\right)} \EE{P e^{-\ou{\alpha}\ell_j} + \oui{\optim}{j} \left(1-e^{-\ou{\alpha}\ell_j}\right)} \\ & = e^{-\ou{\alpha}(\ell_i + \ell_j)} \EE{P^2} - e^{-\ou{\alpha}(\ell_i + \ell_j)} \EE{P}^2 \\ & = e^{-\ou{\alpha} d_{i,j}} \VV{P} \\ & = \frac{\ou{\sigma}^2}{2\ou{\alpha}}\left(1 - e^{-2\ou{\alpha} t_{i,j} }\right) \times e^{-\ou{\alpha} d_{i,j}}. \end{aligned} \end{equation*}\]

Cette expression reste valable quelque soit le niveau de parenté entre \(i\) et \(j\). Ainsi, pour un arbre ultramétrique de longueur \(h\), la matrice de variance-covariance du vecteur gaussien des feuilles (numérotées de 1 à \(m\)) est composée des éléments

\[\begin{equation} \tag{4.1} \frac{\ou{\sigma}^2}{2\ou{\alpha}}\left(e^{-\ou{\alpha} d_{i,j}} - e^{-2\ou{\alpha} h}\right). \end{equation}\]

En particulier, la variance à toutes les feuilles est \(\frac{\ou{\sigma}^2}{2\ou{\alpha}}\left(1 - e^{-2\ou{\alpha} h}\right)\).

4.2 Zazou

4.2.1 Modèle

L’approche que nous avons développée s’appuie sur les \(z\)-scores aux feuilles et fait deux hypothèses :

1. les \(z\)-scores sont la réalisation d’un processus d’Ornstein-Uhlenbeck avec sauts sur l’arbre phylogénétique,
2. sous \(\mathcal{H}_1\), \(\zs_i \sim \normal{\mu_i}{1}\) avec \(\mu_i < 0\).

La première hypothèse nous permet de définir la distribution jointe des \(z\)-scores comme

\[\begin{equation*} \zs \sim \mathcal{N}_{m}\left(\mu,\Sigma\right) \end{equation*}\]

où \(\mu\) dépend de \(\shifts\), le vecteur des sauts du processus, via la relation \(\mu = T\delta\) et \(\Sigma\) dépend de \(\ou{\alpha}\) et \(\ou{\sigma}\) via l’équation (4.1).

La seconde hypothèse est classique lorsqu’on travaille sur les \(z\)-scores (McLachlan & Peel, 2004) et est justifiée par le décalage à gauche des \(p\)-valeurs sous \(\mathcal{H}_1\) : \(\pv_i \preccurlyeq \unif{\mathopen[0, 1\mathclose]}\). Cette hypothèse implique alors l’équivalence entre trouver les hypothèses alternatives et déterminer les composantes non-nulles du vecteur \(\mu\). Sous \(\mathcal{H}_0\) et \(\mathcal{H}_1\), la variance aux feuilles doit valoir \(1\), ce qui impose \[\begin{equation*} \ou{\sigma}=\frac{2\ou{\alpha}}{1 - e^{-2\ou{\alpha}h}}, \end{equation*}\]

de sorte que \(\Sigma\) dépend uniquement de \(\ou{\alpha}\).

À ce stade, nous n’avons accès qu’au vecteur \(\zs\).

4.2.2 Estimation ponctuelle

En supposant \(\ou{\alpha}\) (et donc \(\Sigma\)) connue, une application naïve du maximum de vraisemblance donnerait

\[\begin{equation*} \hat{\mu} = \argmin_{\mu\in\mathbb{R}_-^m} \|\zs - \mu\|_{\Sigma^{-1}, 2}^2 \end{equation*}\]

comme estimateur de \(\mu\). En réalité, c’est la position des sauts qui nous intéresse et nous souhaitons donc plutôt avoir un estimateur de \(\shifts\). En utilisant la relation \(\mu = T\shifts\), celui-ci est donné par

\[\begin{equation*} \hat{\delta} = \argmin_{\shifts \in \shiftset} \left\|\zs - T\shifts\right\|_{\Sigma^{-1},2}^2, \end{equation*}\]

où \(\shiftset = \left\{\shifts\in \mathbb{R}^{n} / T\shifts \in\mathbb{R}_-^m\right\}\) est l’ensemble de faisabilité pour les sauts qui induisent des composantes négatives aux feuilles. Bien que le problème soit convexe (la fonction objective est convexe, tout comme l’ensemble de faisabilité), la matrice \(T\) n’est pas de plein rang et l’estimateur \(\hat{\mu}\) n’est donc pas unique.

Nous lui préférons donc un estimateur parcimonieux, obtenu en rajoutant une contrainte \(\ell_1\) (Tibshirani, 1996) à la fonction objectif :

\[\begin{equation*} \hat{\shifts} = \argmin_{\shifts \in \shiftset} \left\|\zs - T\shifts\right\|_{\Sigma^{-1},2}^2 + \lambda \|\shifts\|_1. \end{equation*}\]

En utilisant la décomposition de Cholesky \(\Sigma^{-1} = R^TR\), ce nouveau problème peut se ramener au problème bien connu du lasso, avec une contrainte convexe sur \(\shifts\) :

\[\begin{equation} \tag{4.2} \hat{\shifts} = \argmin_{\shifts \in \shiftset} \left\|y - X\shifts\right\|_2^2 + \lambda \|\shifts\|_1, \end{equation}\]

où \(y = R\zs \in \RR^m\) et \(X = RT \in \RR^{m \times n}\).

Le problème (4.2) est convexe en \(\shifts\) et sa résolution est possible avec l’algorithme détaillé dans la section 5.1, qui est une modification de l’algorithme du shooting (Fu, 1998).

Il reste maintenant à déterminer \(\ou{\alpha}\) et \(\lambda\). Ceux-ci ne pouvant être obtenus directement à partir des données, nous allons sélectionner le couple qui minimise le critère BIC suivant :

\[\begin{equation*} \left(\ou{\hat{\alpha}}, \hat{\lambda}\right) = \argmin_{\alpha > 0, \lambda \geq 0} \left\|\zs - T\shifts_{\alpha, \lambda}\right\|_{\Sigma(\alpha)^{-1},2}^2 + \log|\Sigma(\alpha)| + \|\shifts_{\alpha, \lambda}\|_0 \log{m}, \end{equation*}\]

où \(\shifts_{\alpha, \lambda}\) est la solution du problème (4.2) pour \(\alpha\) et \(\lambda\). En pratique, une grille bidimensionnelle donne les valeurs du couple à tester. Cette approche a été préférée à l’alternative usuelle de la validation croisée pour ne pas avoir à gérer la dépendance entre les \(z\)-scores.

4.2.3 Débiaisage et intervalles de confiance

L’estimateur lasso est connu pour être biaisé (Javanmard & Montanari, 2013) et ne produit pas d’intervalles de confiance pour les \(\hat{\shifts}_i\). Nous utilisons donc une procédure de débiaisage, comme celles proposées dans Zhang & Zhang (2014) ou Javanmard & Montanari (2013) et Javanmard & Montanari (2014). Ces deux procédures fonctionnent suivant le même principe. Tout d’abord, au lieu d’avoir un estimateur initial de \(\shifts\) comme dans (4.2), nous avons besoin d’un estimateur couplé de \(\shifts\) et de sa variance \(\sigma\), qui peut être obtenu par un scaled lasso (Sun & Zhang, 2012) et qui sera notre estimateur initial :

\[\begin{equation*} \left(\hat{\shifts}^{\text{(init)}},\ \hat{\sigma}\right) = \argmin_{\shifts \in \shiftset, \sigma > 0} \frac{\|y - X \shifts\|_2^2}{2\sigma m} + \frac{\sigma}{2} + \lambda \|\shifts\|_1. \end{equation*}\]

L’estimation jointe est faite de façon itérative en alternant des étapes de mise à jour de \(\hat{\shifts}^{\text{(init)}}\) par lasso et de mise à jour de \(\hat{\sigma}\) par résolution exacte, via l’expression \(\hat{\sigma} = \frac{\left\|y - X \hat{\shifts}^{\text{(init)}}\right\|_2}{\sqrt{m}}\). Une fois cette estimation initiale obtenue, Zhang & Zhang (2014) proposent de calculer un système de score \(S\), qu’on peut comprendre comme une orthogonalisation faible de \(X\), pour corriger \(\hat{\shifts}^{\text{(init)}}\). La colonne \(s_j\) de \(S\) s’obtient comme étant le résidu de la régression lasso de \(x_j\) contre \(X_{-j}\), le reste des colonnes de \(X\).

Puis, l’estimateur débiaisé s’obtient alors en en corrigeant \(\hat{\shifts}_j^{\text{(init)}}\) comme suit :

\[\begin{equation*} \hat{\shifts}_j = \hat{\shifts}_j^{\text{(init)}} + \frac{\langle s_j,y-X\hat{\shifts}^{(\text{init})}\rangle}{\langle s_j,x_j\rangle}. \end{equation*}\]

Javanmard & Montanari (2013) et Javanmard & Montanari (2014) proposent une correction alternative

\[\begin{equation*} \hat{\shifts} = \hat{\shifts}^{(\text{init})} + \frac{1}{m}SX^T \left(Y-X\hat{\shifts}^{(\text{init})}\right), \end{equation*}\]

basée sur un système de score différent. La matrice \(S\) est cette fois-ci un inverse généralisé de \(M = \frac{X^TX}{m}\), construit colonne par colonne en résolvant les problèmes suivants :

\[\begin{equation*} \left\{ \begin{aligned} s_j & = \argmin_{s \in \mathbb{R}^{n}} \ s^TMs \\ &\text{t.q.}\ \|Ms - e_j\|_{\infty} \leq \gamma \end{aligned} \right. \end{equation*}\]

où \(e_j \in \RR^n\) est le \(j^{\text{ème}}\) vecteur de la base canonique définie par \(e_{ij} = \delta_{i,j}\). Dans chacune des deux méthodes, sous des hypothèses standard en régression en grande dimension, \(\hat{\shifts}\sim \mathcal{N}_n\left(\shifts,V\right)\) ce qui permet d’obtenir un intervalle de confiance bilatéral au niveau \(\alpha\) pour \(\shifts_j\) :

\[\begin{equation*} \left[ \hat{\shifts}_j \pm \phi^{-1}\left(1-\frac{\alpha}{2}\right) \sqrt{v_{j,j}} \right]. \end{equation*}\]

Avec le premier système de score, \(V\) se calcule élément par élément :

\[\begin{equation*} v_{i,j} = \hat{\sigma}^2 \frac{\langle s_i,s_j\rangle}{\langle s_i,x_i\rangle\langle s_j,x_j\rangle}, \end{equation*}\]

tandis qu’avec le second, \(V = \frac{S M S^T }{m}\). En exprimant la \(i^{\text{ème}}\) composante de \(\mu\) à l’aide de \(\optim\) comme étant \(\mu_i = t_{i.}^T\shifts\) où \(t_{i.}\) est la \(i^{\text{ème}}\) ligne de \(T\), on obtient également un intervalle de confiance unilatéral au niveau \(\alpha\) pour \(\hat{\mu}_i\) :

\[\begin{equation*} \left[-\infty, \hat{\mu}_i + \sqrt{t_{i.}^T V t_{i.}} \phi^{-1}\left(1-\alpha\right)\right], \end{equation*}\]

et la \(p\)-valeur associée à cet intervalle, qui teste \(\mathcal{H}_0 = \left\{\mu_i = 0\right\}\) contre \(\mathcal{H}_1 = \left\{\mu_i < 0\right\}\), est donc

\[\begin{equation*} \pv^\text{h}_i = \Phi\left(\frac{t_{i.}^T\hat{\shifts}}{\left(t_{i.}^TVt_{i.}\right)^{1/2}}\right), \end{equation*}\]

qui est la \(p\)-valeur lissée hiérarchiquement.

4.2.4 Correction pour tests multiples

Une fois ces \(p\)-valeurs lissées obtenues, Javanmard, Javadi, & others (2019) proposent une méthode de correction pour tests multiples conçue spécialement pour le lasso débiaisé et qui repose sur les \(t\)-scores \(\ts_i = \frac{t_{i.}^T\hat{\shifts}}{\left(t_{i.}^TVt_{i.}\right)^{1/2}}\).

Définissons \(t_{\text{max}} = \sqrt{2 \log m - 2 \log \log m}\) puis

\[\begin{equation} \tag{4.3} t^{\star} = \inf \bigg\{ 0 \leq t \leq t_{\max} : \underbrace{\frac{2m(1 - \Phi(t))}{R(t) \vee 1}}_{\widehat{\text{FDR}}(t)} \leq \alpha \bigg\}, \end{equation}\]

où \(R(t)= \sum_{i = 1}^m \indic_{\{\ts_i \leq -t\}}\) est le nombre d’hypothèses nulles rejetées au niveau \(t\). Le numérateur du quotient peut s’interpréter comme le nombre attendu de rejets sous l’hypothèse nulle, et celui-ci est donc une estimation du \(\text{FDR}\) au niveau \(t\), que l’on cherche à garder sous le seuil \(\alpha\). Si l’infimum en (4.3) est \(+\infty\), on pose \(t^{\star} = \sqrt{2 \log m}\).

On rejette \(\mathcal{H}_0\) si \(\ts_i \leq -t^{\star}\) ce qui amène à définir les \(q\)-valeurs hiérarchiques \[\begin{equation*} \qv^{\text{h}}_i = \frac{\pv^{\text{h}}_i \alpha}{\Phi(-t^{\star})}, \end{equation*}\] et l’hypothèse nulle associée est rejetée si \(\qv^{\text{h}}_i < \alpha\). Cette procédure contrôle le FDR au niveau \(\alpha\) (Javanmard et al., 2019).

Remarque. Comme \(t^{\star}\) dépend de \(\alpha\), les \(q\)-valeurs dépendent aussi de \(\alpha\) et doivent être calculées pour chaque niveau de FDR cible, contrairement à la procédure BH(\(\alpha\)) standard.

4.3 Évaluation de la méthode

4.3.1 Données simulées

Afin d’évaluer la qualité de notre procédure, nous avons simulé des données de manière non-paramétrique, comme présenté dans la section 3.4.3 et dans la figure 3.7 : à partir d’un jeu de données homogènes, on sélectionne des taxons différentiellement abondants, on assigne un groupe \(A\) ou \(B\) à chacun des échantillon et on multiplie les abondances de chaque taxon différentiellement abondant dans le groupe \(B\) par un fold-change prédéterminé.

Trois déclinaisons de simulations ont été adoptées. Dans la première, dite positive, les taxons sont sélectionnés pour former des groupes dans la phylogénie et un fold-change de \(3\), \(5\) ou \(10\) est ensuite appliqué. Ceci permet de créer des simulations pour lesquelles l’arbre est réellement informatif. Plus précisément, pour sélectionner les taxons différentiellement abondants, on applique un algorithme des \(k\)-médoïdes (Reynolds, Richards, Iglesia, & Rayward-Smith, 2006) à la matrice des distances patristiques (Sneath, Sokal, & others, 1973), ce qui donne des groupes de taxons à faible distance patristique les uns des autres, qui correspondent généralement à un sous-arbre de la phylogénie. Un ou plusieurs groupes sont alors sélectionnés aléatoirement et leurs taxons sont déclarés différentiellement abondants.

Les deux autres déclinaisons de la procédure de simulation de jeux de données sont dites négatives. Pour l’une, les taxons sont sélectionnés uniformément dans l’arbre puis un fold-change de \(5\) est appliqué, pour créer des simulations dans lesquelles le modèle est mal spécifié. Pour l’autre le fold-change appliqué vaut \(1\), ce qui permet de voir comment réagit l’algorithme lorsqu’aucun taxon n’est différentiellement abondant.

La figure 4.2 présente les résultats dans le cas des simulations positives. Si les procédures de corrections classiques (BH et BY) contrôlent bien le FDR à \(5~\%\), ce n’est pas le cas pour les procédures hiérarchiques. Dans la majorité des cas, le FDR des procédures hiérarchiques reste en dessous de \(6~\%\) mais pour la procédure à système de score (ss) avec un fold-change de \(5\) et pour celle avec l’inverse généralisé par colonne (ci) avec un fold-change de \(3\), il passe à \(8\) et \(9~\%\) respectivement. Dans toutes les configurations, BY a le TPR le plus faible, BH et TreeFDR (tf) se comportent de manière semblable, conformément aux résultats présentés dans Bichat et al. (2020), et les deux variantes de zazou obtiennent le meilleur TPR.

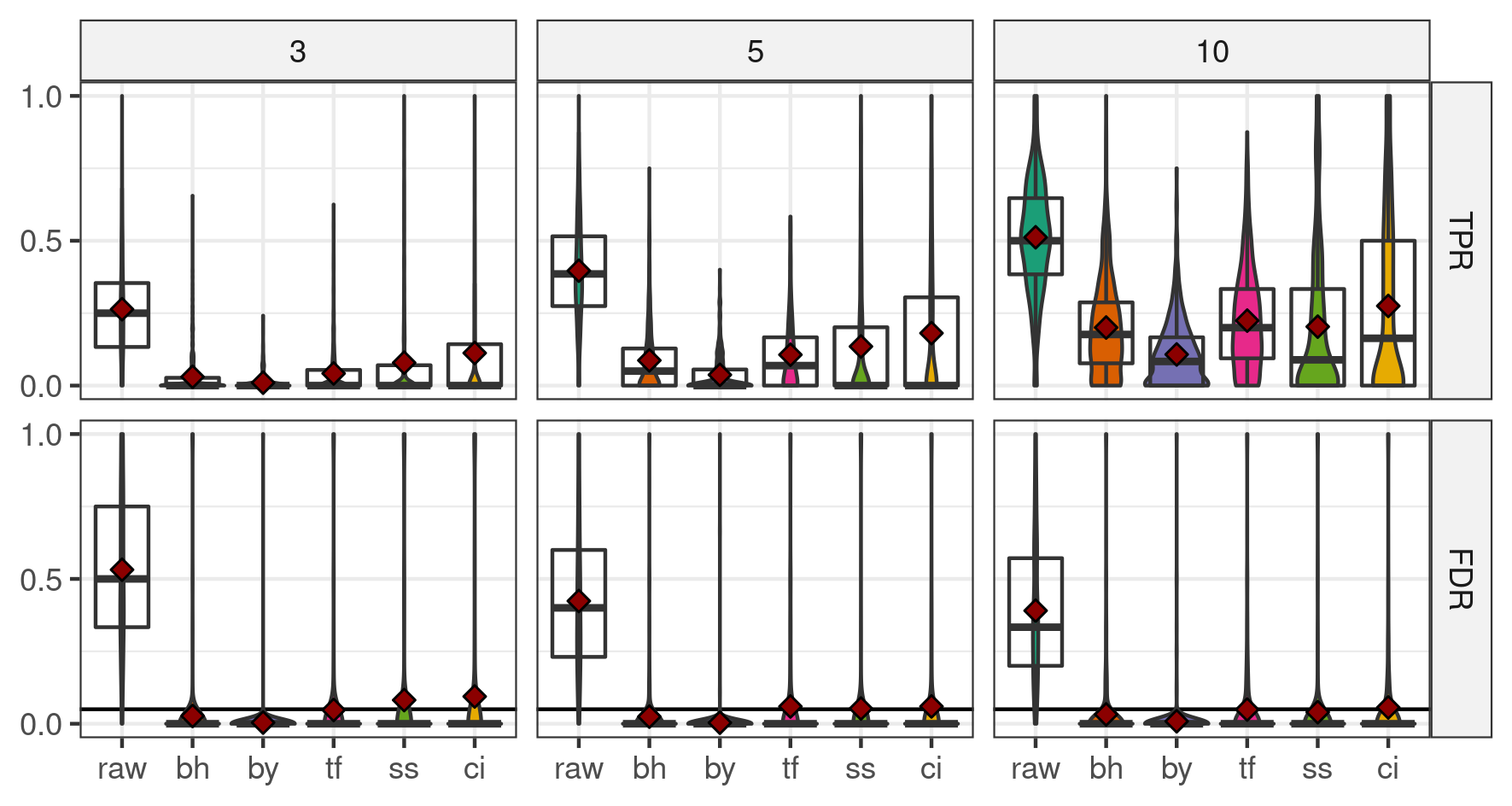
Figure 4.2: TPR (haut) et FDR (bas) pour les différentes procédures et différents fold-changes (en colonnes) dans le cadre des simulations positives.

Le taux de faux positif plus élevé qu’attendu pour les résultats de zazou suggère que le choix du seuil de détection proposé dans Javanmard et al. (2019) n’est pas complètement adapté. Nous comparons donc les performances des différentes méthodes à l’aide de l’AUC, qui est une mesure indépendante du seuil. La figure 4.3 met en évidence les meilleures performances de zazou, dans ses deux variantes. En regardant la partie gauche des courbes ROC, on s’aperçoit que zazou est plus performant dès les premières découvertes et que cela n’est pas un effet compensatoire des seuils plus élevés. Comme mentionné précédemment, BH et TreeFDR obtiennent des performances similaires et moins bonnes que celles de zazou. BY est la méthode la moins satisfaisante (du fait du grand nombre de \(p\)-valeurs ajustées à \(1\)).

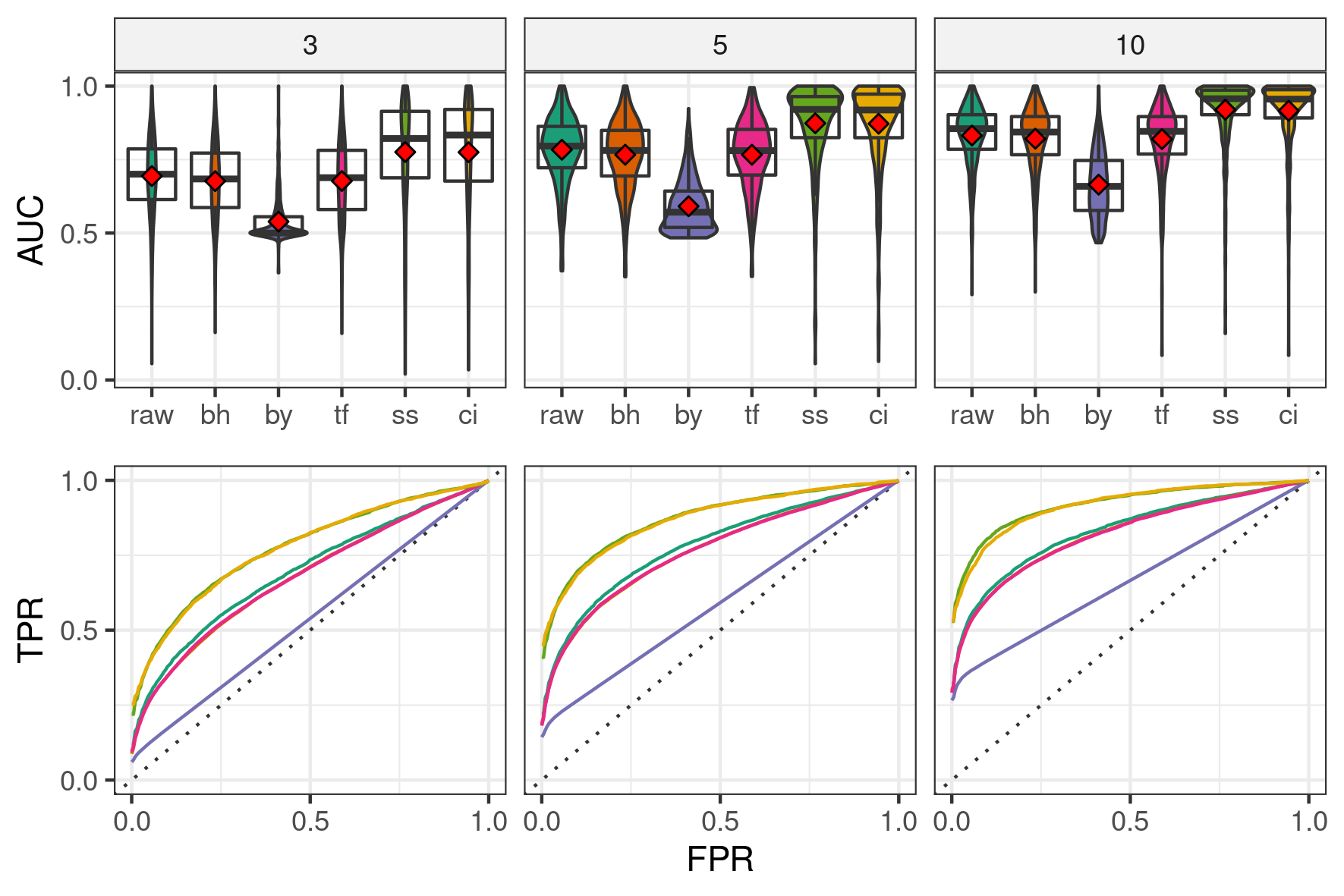
Figure 4.3: Distribution des AUC (haut) et courbes ROC (bas) pour les différentes procédures et fold-changes (en colonnes) dans le cadre des simulations positives.

Dans le cas des simulations négatives (figure 4.4), l’imposition d’une contrainte hiérarchique inadaptée fait perdre \(15\) à \(20\) points d’AUC à zazou par rapport à BH. Ce phénomène ne se retrouve pas dans les résultats de TreeFDR, qui est pourtant également une procédure hiérarchique, grâce à une astuce d’implémentation. En effet, TreeFDR effectue une correction de BH en parallèle de la procédure de lissage, et si cette dernière détecte bien moins de taxons que BH, les résultats de BH sont renvoyés à la place de ceux obtenus par lissage (Bichat et al., 2020; Xiao et al., 2017).

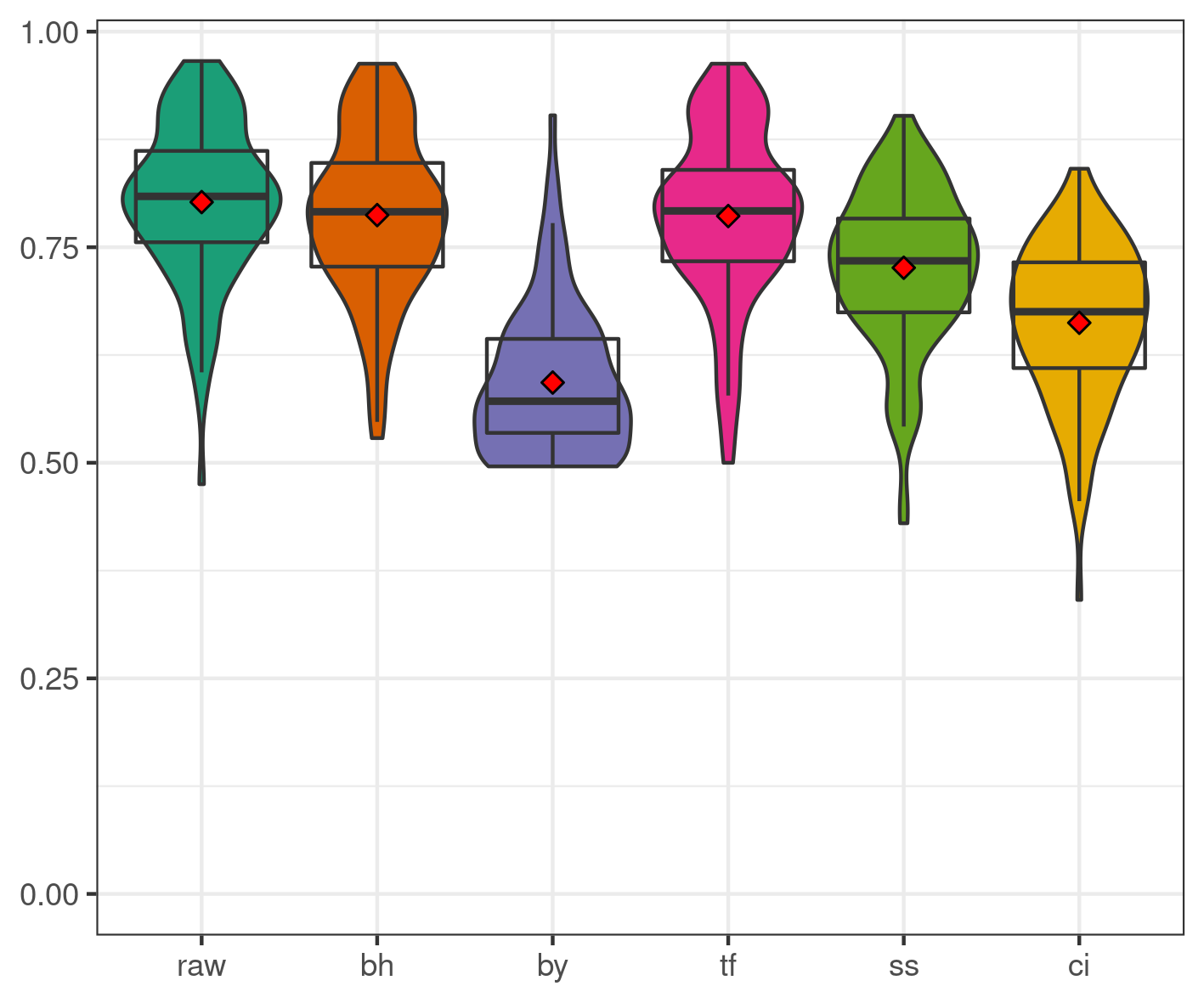
Figure 4.4: Distribution des AUC pour les différentes procédures lorsque les taxons différentiellement abondants sont sélectionnés uniformément.

Enfin, pour les simulations où aucun taxon n’est différentiellement abondant (\(\text{fc} = 1\)), les procédures ne détectent aucun faux positif, comme attendu.

4.3.2 Influence de l’âge

Nous avons comparé l’effet des différentes procédures de correction lors d’une analyse d’abondance différentielle entre des \(112\) adultes et \(34\) enfants au sein du jeu de données de Brito et al. (2016) des populations insulaires. Des tests de Wilcoxon ont été effectués sur les 387 espèces présentes et 21 espèces ont été détectées à \(5~\%\) sans correction. Après correction par BH, BY, TreeFDR ou treeclimbR, aucune espèce n’est détectée. En revanche, zazou en détecte certaines avec ses deux variantes : 17 pour ss et 6 pour ci.

La figure 4.5 montre que les espèces détectées par zazou ne forment pas un sous-ensemble de celles obtenues sans correction. Au contraire, zazou identifie des espèces proches de certaines détectées sans correction, majoritairement dans la zone mise en évidence par le bandeau rouge.

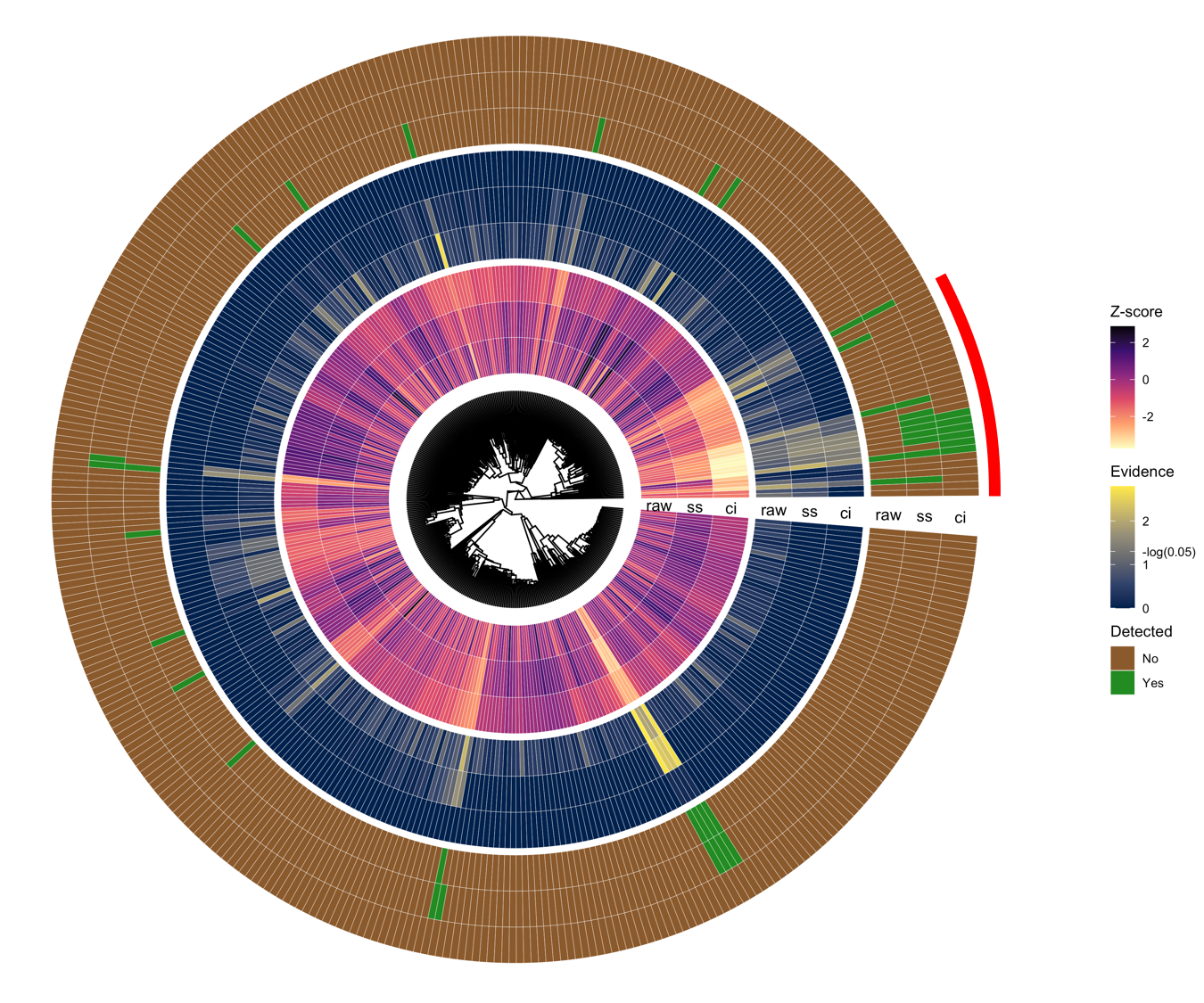
Figure 4.5: Phylogénie des \(387\) espèces du jeu de données des Fidjiens. Les cercles intérieur, central et extérieur représentent respectivement les \(z\)-scores bruts, les évidences corrigées et les statuts détecté ou non associé aux espèces pour différentes procédures (sans correction et les deux variantes de zazou).