Chapitre 3 Arbres

3.1 Définitions

Un arbre est un graphe connexe acyclique. Les nœuds de degré \(1\) sont appelés feuilles, par oppositions aux nœuds internes.

Un arbre enraciné est un graphe connexe acyclique dirigé possédant une unique racine. Chaque nœud \(i\), à l’exception de la racine, a un unique parent noté \(\pa(i)\). Les feuilles sont les nœuds n’ayant pas de fils. Il est possible d’enraciner un arbre non-raciné en choisissant un nœud quelconque et en orientant les arêtes de la racine vers les feuilles. La branche menant au nœud \(i\) est dénotée \(b_i\) et a pour longueur \(\ell_i\). On parle de topologie d’un arbre lorsqu’on fait abstraction de ses longueurs de branche.

On note \(\mrca(i,j)\) l’ancêtre commun le plus récent (most recent common ancestor) aux nœuds \(i\) et \(j\) : \(\mrca(i,j) = \pa^k(i)\), soit le \(k\)-ième parent successif de \(i\), avec \(k = \argmin_{p\in \NN}\left\{\exists q \in \NN : \pa^p(i) = \pa^q(j)\right\}\), et \(\desc(i)\) les descendants de \(i\), soit l’ensemble des nœuds ayant \(i\) pour ancêtre, \(i\) inclus : \(\desc(i) = \left\{j : \exists k \in \NN : \pa^k(j)=i\right\}\).

Le nœud \(i\) est à distance \(t_i\) de la racine et on note \(t_{i,j} = t_{\mrca(i,j)}\).

La distance, dite patristique, entre les nœuds \(i\) et \(j\) est notée \(d_{i,j} = t_i + t_j - 2 t_{i,j}\).

\(\tilde{\ell}_{i,j} = t_i - t_{i,j}\) est la distance entre le nœud \(i\) et l’ancêtre commun le plus récent à \(i\) et \(j\).

Un arbre enraciné est binaire si tous ses nœuds internes ont exactement deux fils. En particulier, un arbre binaire à \(m\) feuilles possède \(n = 2m-2\) branches.

Un nœud est polytomique s’il a plus de deux fils.

Un arbre est ultramétrique s’il est raciné et si toutes les feuilles sont à la même distance de la racine.

Un clade est un sous-arbre, il contient un nœud et tous ses descendants.

Pour un arbre enraciné, la matrice d’incidence \(T = (t_{i,j}) \in\{0,1\}^{m \times n}\) encode les relations de descendance entre nœuds au sein de l’arbre. Pour une feuille \(i\) et un nœud quelconque \(j\), le coefficient \(t_{i,j}\) vaut \(1\) si \(i \in \desc(j)\). En particulier, la colonne \(t_j\) est l’indicatrice des feuilles issues du nœud \(j\) tandis que la ligne \(t_{i.}\) est l’indicatrice des ancêtres de la feuille \(i\).

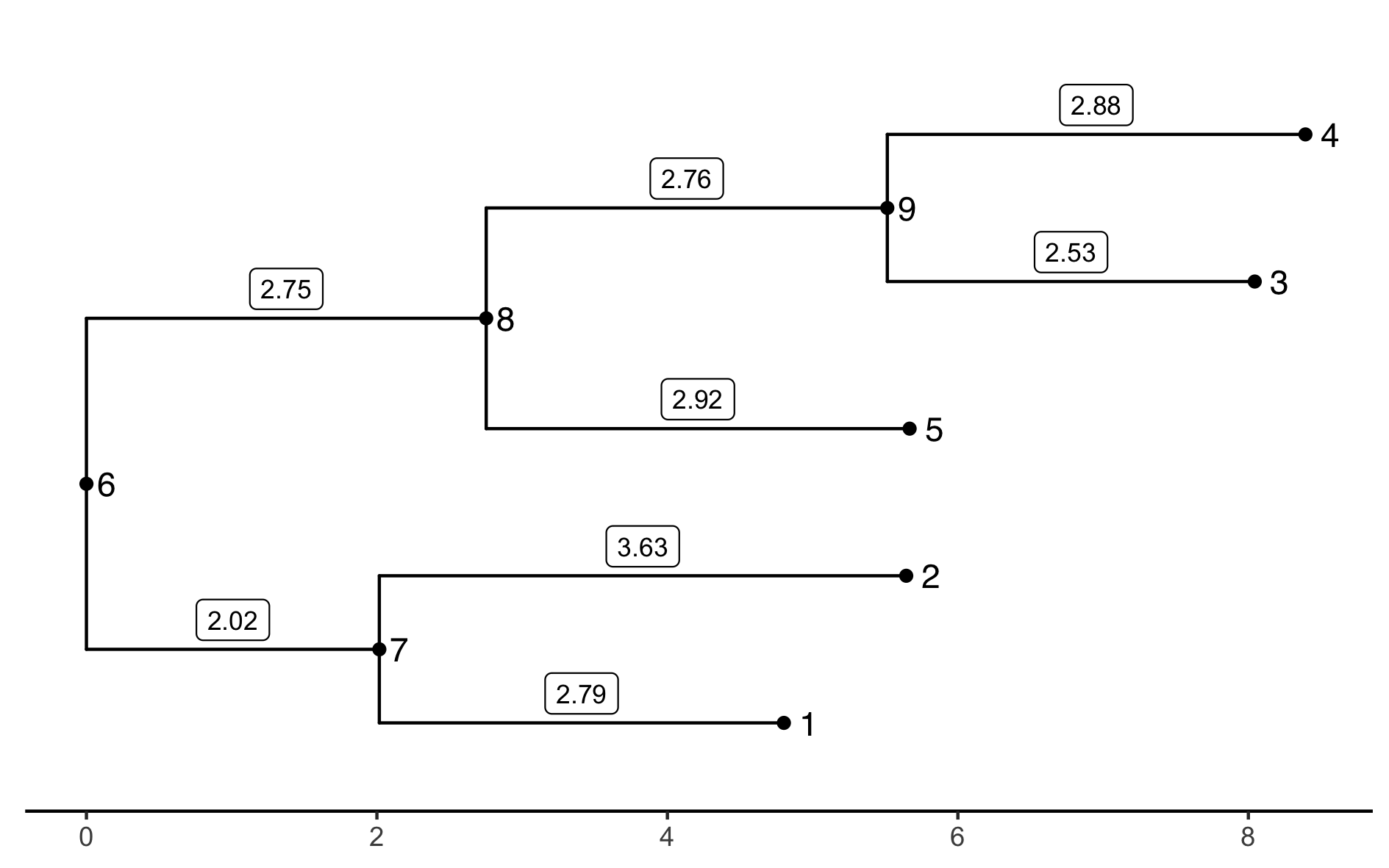
Figure 3.1: Exemple d’un arbre enraciné binaire non ultramétrique à \(m = 5\) feuilles et \(n = 8\) branches.

Illustrons les notations de cette section à l’aide de la figure 3.1. On a alors \(\pa(1) = \pa(2) = 7\), \(\desc(8) = \{3, 4, 5, 8, 9\}\), \(\mrca(5, 3) = 8\), \(\ell_1 = 2.79\), \(t_{3,4} = t_9 = \ell_8 + \ell_9 = 5.51\), \(t_{1,2} = t_7 = 2.02\), \(d_{3,5} = t_3 + t_5 - t_{3,5} = \ell_5 + \ell_9 + \ell_3 = 8.21\), \(\tilde{\ell}_{3,5} = t_3 - t_{3,5} = \ell_9 + \ell_3 = 5.29\) et

\[\begin{equation*} T = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 \\ \end{bmatrix}. \end{equation*}\]

3.2 Distances

Les arbres sont des objets compliqués et plusieurs distances entre arbres ont été proposées dans la littérature. Nous en décrivons brièvement trois, qui mettent l’accent sur des aspects différents de l’arbre: topologie, longueurs de branche, combinaison des deux.

3.2.1 Distance de Robinson-Foulds

La distance de Robinson-Foulds (Robinson & Foulds, 1981) entre deux arbres racinés \(T\) et \(T'\) correspond intuitivement au nombre de branches spécifiques à un des deux arbres. Formellement, chaque nœud interne \(j\) définit une bipartition des feuilles et peut être associé à l’ensemble \(C_j \subset [\![1,m]\!]\) des feuilles issues du nœud \(j\). La colonne \(j\) de la matrice d’incidence précédemment introduite correspond en particulier à un codage binaire de \(C_j\). L’arbre \(T\) est ensuite recodé comme l’ensemble \(\mathcal{C}^T = \{C_j: j \in \text{nœud interne de } T\}\) de ses bipartitions. La distance de Robinson-Foulds entre \(T\) et \(T'\) est définie comme le cardinal de la différence symétrique entre \(\mathcal{C}^T\) et \(\mathcal{C}^{T'}\) :

\[\begin{equation*} d(T, T') = | \mathcal{C}^T \setminus \mathcal{C}^{T'} | + | \mathcal{C}^{T'} \setminus \mathcal{C}^{T} |. \end{equation*}\]

3.2.2 Distance cophénétique

La distance cophénétique entre deux arbres enracinés, introduite par Sokal & Rohlf (1962), est basée sur les matrice des distances patristiques \(D^T = \left(d^T_{i,j}\right)_{i,j}\) entre paires de feuilles dans l’arbre \(T\), en particulier sur la vectorisation \(v^T\) de la partie triangulaire supérieure de \(D^T\), de longueur \(\frac{m(m-1)}{2}\). La distance cophénétique \(d(T, T')\) entre arbres \(T\) et \(T'\) est définie comme le complémentaire du coefficient de corrélation de Pearson entre \(v^{T_1}\) et \(v^{T_2}\):

\[\begin{equation*} d(T, T') = 1 - \frac{ \frac{2\sum_{i < j} (d^{T}_{i,j} - \bar{d}^{T})(d^{T'}_{i,j} - \bar{d}^{T'})}{m(m-1)}}{\sqrt{\frac{2\sum_{i < j} (d^{T}_{i,j} - \bar{d}^{T})^2}{m(m-1)}} \sqrt{\frac{2\sum_{i < j} (d^{T'}_{i,j} - \bar{d}^{T'})^2}{m(m-1)}}} = 1 - \text{cor}(v^T, v^{T'}) \end{equation*}\]

où \(\bar{d}^{T} = \frac{2}{m(m-1)} \sum_{1 \leq i < j \leq m} d^{T}_{i,j}\). Cette distance ne prend en compte que la topologie de l’arbre.

3.2.3 Distance de Billera-Holmes-Vogtmann (BHV)

La distance BHV (Billera, Holmes, & Vogtmann, 2001) est construite en plongeant l’espace \(\mathscr{T}_m\) des arbres à \(m\) feuilles dans \(\RR^m \times \RR^{2^{m}-m-1}\) puis en considérant la distance des plus courts chemins dans le sous-espace induit.

Formellement, un arbre binaire est définie par (i) sa topologie et (ii) ses longueurs de branches. Il existe \(m\) branches terminales (menant à une feuille) et \(2^{m} - m - 1\) branches internes distinctes, caractérisées chacune par l’ensemble des feuilles issues de cette feuille. Toutes ces branches ont une longueur positive. L’espace \(\mathscr{T}_m\) est donc naturellement plongé dans \(\RR_+^m \times \RR_+^{2^{m}-m-1}\). Le produit cartésien distingue les longueurs des branches externes (celles qui mènent aux feuilles, partagées par tous les arbres) de celles des branches internes, caractéristique d’une topologie donnée. Mais il n’en constitue qu’une sous-variété. En effet, à topologie \(T\) fixée, chaque longueur de branche peut varier dans \(\RR_+\). L’ensemble des arbres binaires de topologie \(T\), branches terminales omises, est donc identifiable à l’orthant ouvert \(\RR_+^{*, m-2}\). Si on fait tendre la longueur d’une branche interne vers \(0\), on se ramène à une topologie non-binaire \(\tilde{T}\), dans laquelle un unique nœud a exactement trois fils. Cette topologie peut également s’obtenir par contraction de branche interne à partir de deux autres topologies binaires \(T'\) et \(T''\). La topologie non-binaire \(\tilde{T}\) correspond à une , un sous-orthant de dimension \(m-3\) inclus dans chacun des trois orthants de dimension \(m-2\) caractérisant \(T\), \(T'\) et \(T''\). De façon générale, les sous-orthants de dimension \(m - 2 - k\) peuvent être identifiés à des topologies dégénérées, obtenues en contractant \(k\) branches internes d’un arbre binaire.

Il existe \((2m-3)!! = (2m-3)\times(2m-5)\times\dots\times5 \times 3 \times 1 = \prod_{i = 0}^{m-2} 2i+1\) topologies binaires (Cavalli-Sforza & Edwards, 1967) qui correspondent à autant d’orthants de dimension \(m-2\). \(\mathscr{T}_m\) est donc constitué de \((2m-3)!!\) orthants (un par topologie) de dimension \(m-2\), entre eux par des sous-orthants de dimension inférieure et correspondant à des topologies non-binaires. La figure 3.2 montre une jonction de tels orthants dans le cas où \(m=4\).

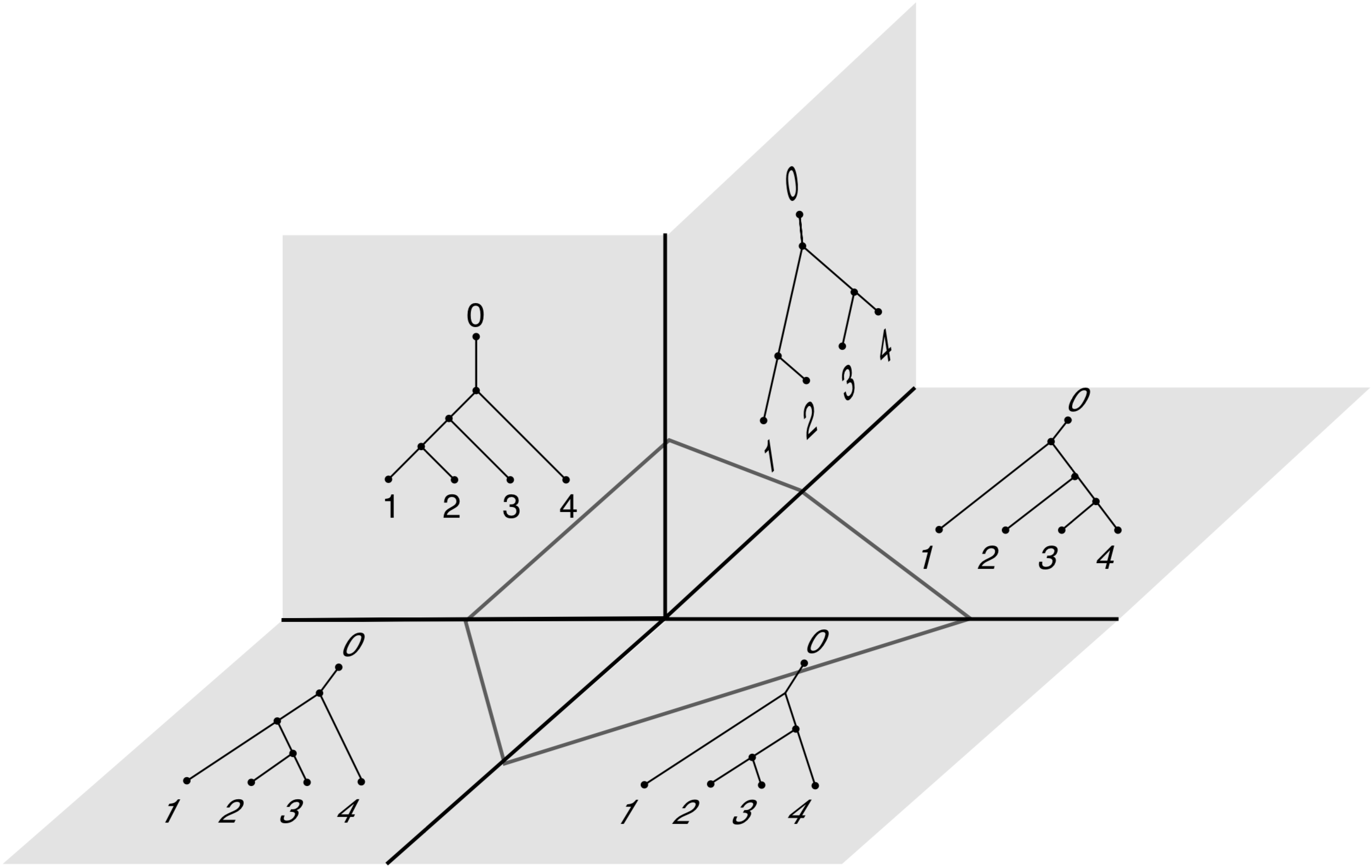
Figure 3.2: Une partie de \(\mathscr{T}_4\), où cinq orthants se rejoignent, tiré de Billera et al. (2001).

Billera et al. (2001) montrent que \(\mathscr{T}_m\) est connexe et possède une courbure négative. En particulier, pour toute paire d’arbres \(T\) et \(T'\), il existe un plus court chemin dans \(\mathscr{T}_m\) entre \(T\) et \(T'\). La distance BHV est la distance géodésique dans \(\mathscr{T}_m\), c’est à dire la distance du plus court chemin. Lorsque \(T\) et \(T'\) appartiennent au même orthant (c’est à dire partagent la même topologie), la distance géodésique coïncide avec la distance euclidienne dans l’orthant.

La figure 3.3 illustre un exemple plus complexe dans lequel le plus court chemin traverse plusieurs orthants. Dans cet exemple, la distance géodésique est la somme des distances euclidiennes du chemin parcouru dans chaque orthant. La distance BHV prend en compte la topologie, les longueurs de branche et la géométrie de \(\mathscr{T}_m\) mais son calcul effectif est nettement plus coûteux que celui des distances cophénétiques et de Robinson-Foulds (Owen & Provan, 2010).

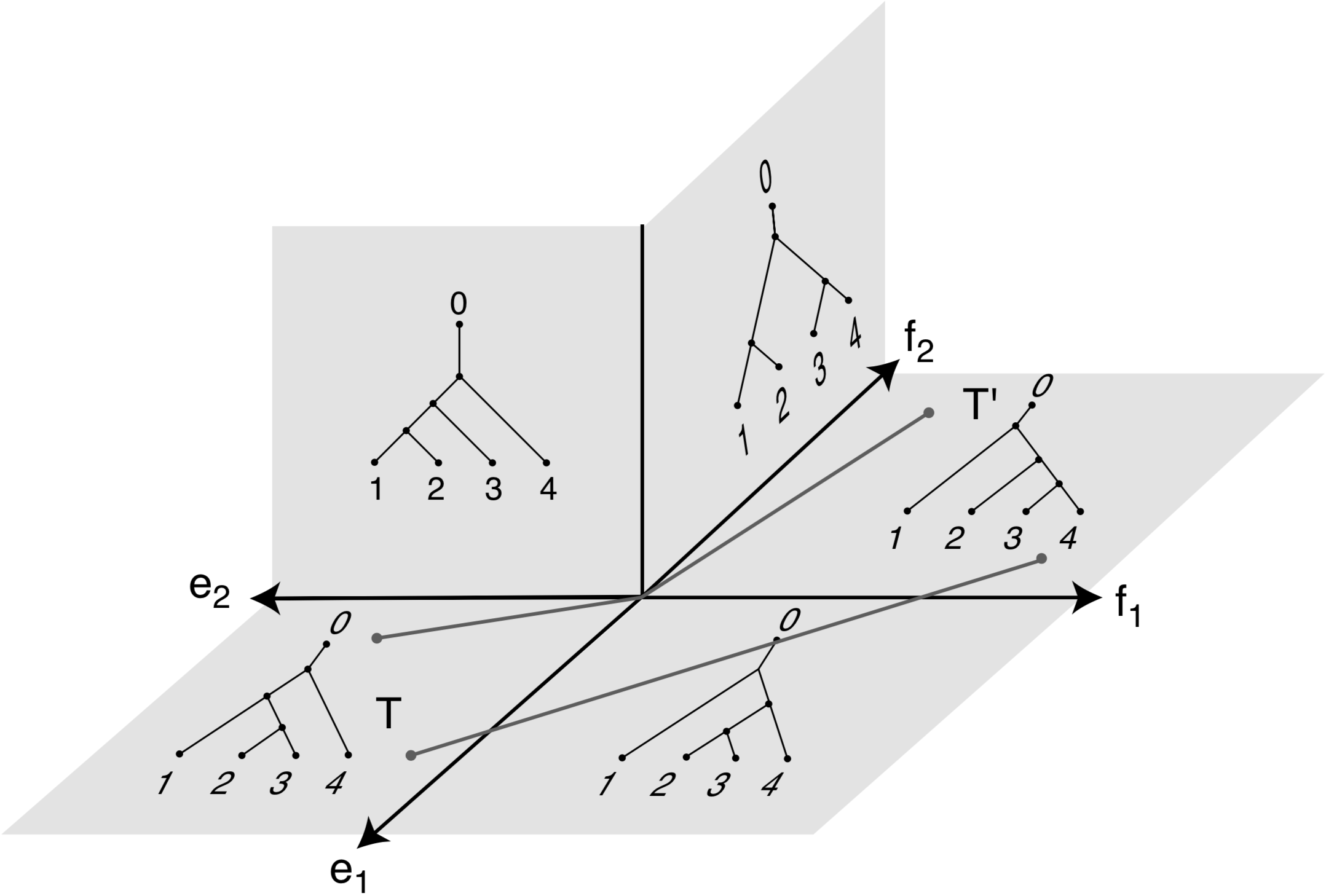
Figure 3.3: Des chemins traversant plusieurs orthants dans \(\mathscr{T}_4\), tiré de Billera et al. (2001).

3.3 Arbres d’intérêt

Dans nos analyses, nous considérons trois types d’arbre : taxonomique, phylogénétique ou de corrélation. Les deux premiers représentent l’histoire évolutive des taxons et sont reconstruits à partir de données phénotypiques et moléculaires. Le dernier est reconstruit à partir des tableaux d’abondance et représente les similarités en terme de profils d’abondance.

3.3.1 Phylogénie

L’arbre phylogénétique, ou phylogénie, traduit les relations de parenté entre organismes. Pour un séquençage avec gène marqueur, l’arbre est reconstruit à partir des séquences représentatives (Price, Dehal, & Arkin, 2010). Intuitivement, la longueur d’une branche reflète la distance évolutive entre une séquence et sa séquence parentale, mesuré par le nombre moyen de substitutions par paire de bases sur la branche.

3.3.2 Taxonomie

La classification linnéenne du vivant regroupe les espèces au sein de groupes cohérents de plus en plus larges : genres, familles, ordres, classes, embranchements et règnes. Cette hiérarchie peut être représentée sous la forme d’un arbre, dit taxonomie, et est disponible dans des bases de données comme celle du NCBI (Geer et al., 2010). Cette taxonomie est construite à partir de données phénotypiques ou moléculaires mais est indépendante des données d’abondance. De plus, l’étiquetage des espèces et des rangs supérieurs permet d’avoir un cadre conceptuel unifié entre différentes études. En revanche, l’arbre n’est pas binaire mais au contraire fortement polytomique et les branches n’ont pas de longueur naturelle. Elles seront arbitrairement fixées à \(1\) dans la suite des analyses.

3.3.3 Arbre des corrélations

Afin de rendre compte de la structure observée des données, nous avons défini un arbre, dit arbre des corrélations, construit à partir des tables d’abondances. Dans un premier temps, la table d’abondance est utilisée pour construire une matrice de dissimilarité \(D = (d_{i,j})\) entre espèces, définie par : \[\begin{equation*} d_{i,j} = 1 - \frac{\text{cov}(\text{rg}_{\tilde{X}_i(i,j)}, \text{rg}_{\tilde{X}_j(i,j)})}{\sigma_{\text{rg}_{\tilde{X}_i(i,j)}} \sigma_{\text{rg}_{\tilde{X}_j(i,j)}}} \end{equation*}\] où \(\text{rg}_X\) désigne les variables de rang du vecteur \(X\) et \(\tilde{X}_{i}(i,j) = \{X_i: X_i + X_j > 0\}\), \(\tilde{X}_{j}(i,j) = \{X_i: X_i + X_j > 0\}\) sont les profils d’abondances de \(X_i\) et \(X_j\) privés des coordonnées simultanément nulles. Le deuxième terme du membre de droite correspond à la corrélation de Spearman entre \(\tilde{X}_{i}(i,j)\) et \(\tilde{X}_{j}(i,j)\). La matrice \(D\) est utilisée pour construire une classification ascendante hiérarchique avec la méthode de Ward. L’arbre des corrélations correspond au dendrogramme de la classification. Par construction, les taxons au profil d’abondance similaire sont regroupés ensemble et la longueur des branches correspond au coût de fusion entre deux sous-arbres.

Contrairement aux arbres taxonomiques et phylogénétiques, l’arbre des corrélations est construit à partir des abondances et il est toujours possible de le calculer, y compris lorsque les « taxons » ne sont pas des espèces mais d’autres entités (gènes, MSPs, etc) pour lesquelles ni la phylogénie, ni la taxonomie ne sont définies.

Cependant, l’arbre des corrélations étant estimé à partir des données, il est sensible à la variabilité de celles-ci. C’est d’autant plus le cas pour les couples d’espèces rares où il y a beaucoup de zéros partagés et l’estimation de leur corrélation est très imprécise. Ce problème peut être résolu en filtrant les espèces à faible abondance ou prévalence mais ce sont souvent ces espèces rares qui jouent un rôle crucial dans le fonctionnement des écosystèmes (Jousset et al., 2017).

Enfin, si les données servent à la fois à construire l’arbre des corrélations et à effectuer les tests, il faut faire attention à ne pas surapprendre de celles-ci.

3.4 Comparaison entre les arbres

Notre objectif est de comparer l’arbre des corrélations à l’arbre taxonomique (ou phylogénétique). Nous nous intéressons plus précisément aux trois questions suivantes :

• L’arbre des corrélations est-il significativement différent de l’arbre taxonomique ?

• L’arbre des corrélations est-il plus proche de l’arbre taxonomique qu’un arbre aléatoire ?

• Quel est l’impact de l’arbre sur les procédures d’abondance différentielle hiérarchiques ?

Pour répondre aux deux premières questions, nous utilisons une forêt d’arbres pour construire une région de confiance autour de l’arbre des corrélations et une distance typique entre arbres aléatoires. Une réponse à la dernière question sera apportée en testant différents choix d’arbre pour les procédures hiérarchiques sur des jeux de données simulées et réelles.

3.4.1 Forêt d’arbres

L’arbre des corrélations étant estimé à partir des données et assez variable, nous déterminons une région de confiance autour de celui-ci à l’aide de la méthode du bootstrap (Felsenstein, 1985; Wilgenbusch, Huang, & Gallivan, 2017). Pour ce faire, nous créons \(N_B\) nouvelles tables d’abondance par un ré-échantillonnage avec remise sur les échantillons (i.e. les colonnes) puis, pour chaque table ainsi construite, nous calculons un nouvel arbre de corrélation.

Nous générons également des arbres aléatoires, sous l’hypothèse nulle, en permutant les labels des feuilles d’un arbre de référence. Cette procédure conserve le nombre de branches et la distribution des polytomies. Elle est de ce fait plus adaptée qu’un tirage uniforme dans l’espace des arbres, qui favorise les topologies symétriques binaires et ne génère pas de nœuds polytomiques. \(N_T\) arbres aléatoires sont générés de cette manière en partant de la taxonomie et \(N_C\) en partant de l’arbre des corrélations.

Au total, nous avons donc une forêt comprenant \(2 + N_B + N_C + N_T\) arbres ayant les mêmes feuilles.

3.4.2 Distance entre les arbres

Nous calculons la matrice des distances RF et BHV entre toutes les paires d’arbres de notre forêt, que nous exploitons de deux façons différentes.

Nous regardons d’abord la distance entre chaque arbre et l’arbre des corrélations. La partie supérieure de la figure 3.4 représente les boîtes à moustaches ainsi que les diagrammes en violon de ces distances pour trois jeux de données. L’arbre des corrélations est significativement plus proche de ses réplicats bootstrapés que de la taxonomie ou des arbres aléatoires (\(\pv<10^{-16}\) avec un test des étendues de Tukey). De plus, la taxonomie est aussi loin de l’arbre des corrélations que peut l’être une taxonomie aléatoire (\(\pv > 0.05\)).

Ensuite, ayant accès à toutes les distances deux à deux nous pouvons également effectuer une analyse en coordonnées principale (PCoA, Principal COmponent Analysis) (Gower, 1966) sur la forêt d’arbres. La PCoA est une méthode de réduction de dimension des données. Comme l’analyse en composantes principale (ACP), elle cherche à construire des axes décorrélés entre eux qui vont maximiser l’inertie du nuage de points. Mais contrairement à l’ACP, la PCoA s’appuie sur une matrice de distances et non sur un tableau de descripteurs individus \(\times\) variables. Dans \(\RR^n\), effectuer une PCoA avec les distances euclidiennes est équivalent à faire une ACP.

Dans la partie inférieure de la figure 3.4, nous avons les deux premiers axes de la PCoA avec la distance BHV pour différents jeux de données, ce que Jombart, Kendall, Almagro-Garcia, & Colijn (2017) et Wilgenbusch et al. (2017) appellent des paysages d’arbres (tree landscapes). Nous apercevons deux ou trois îlots (Jombart et al., 2017) : un pour l’arbre de corrélations et ses réplicats bootstrapés, qui matérialisent sa région de confiance, un pour la taxonomie et les taxonomies aléatoires et un dernier pour les arbres aléatoire construits à partir de l’arbre des corrélations –les deux derniers étant éventuellement confondus, comme c’est le cas pour les données de Ravel et al. (2011). Bien que le premier axe ne représente que \(5\) à \(10~\%\) de l’inertie totale, il exclut systématiquement la taxonomie de la région de confiance de l’arbre des corrélations.

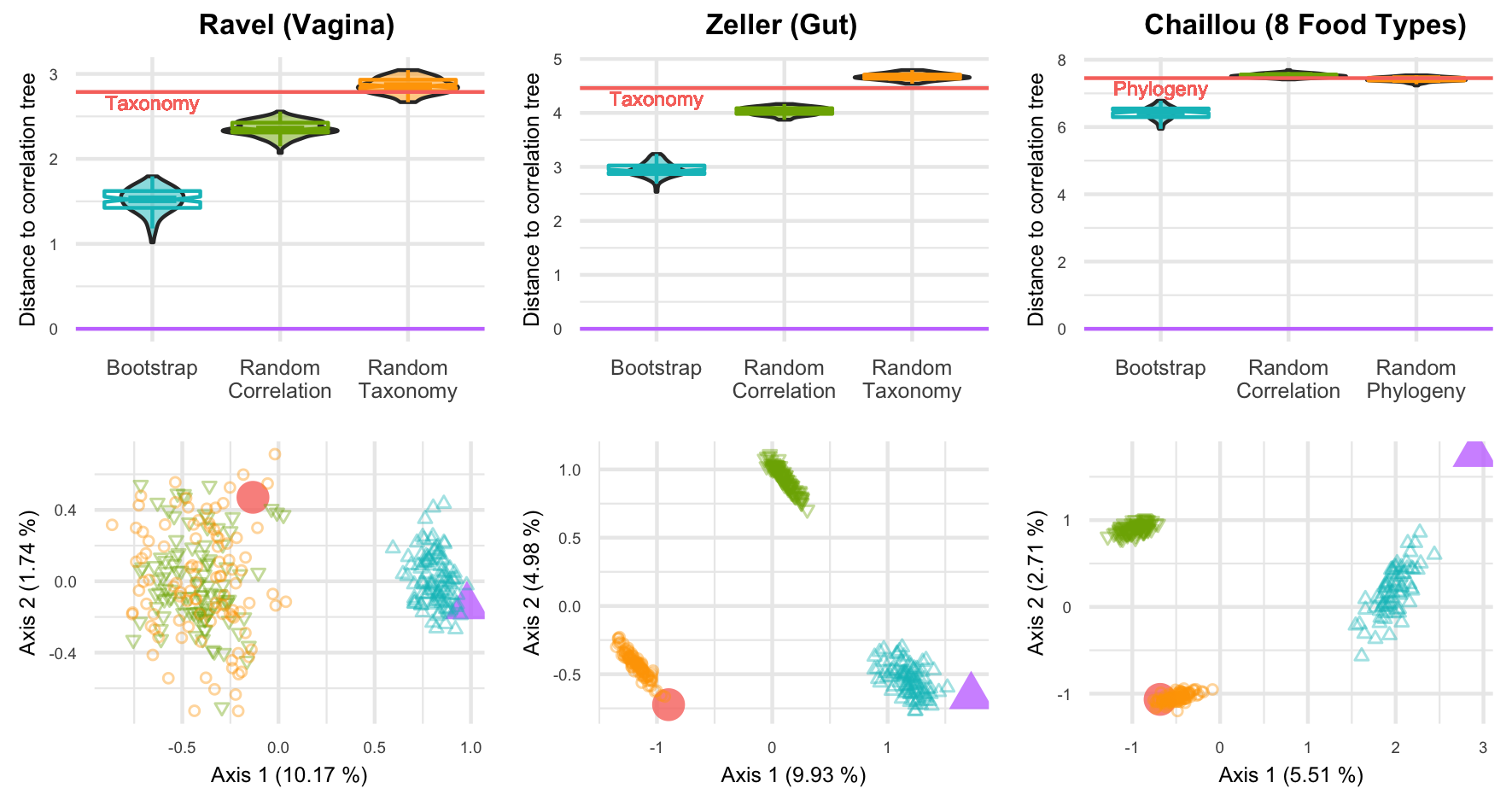
Figure 3.4: Distances BHV au sein de la forêt d’arbres pour trois jeux de données.

Ces résultats doivent être mis en regard de ceux obtenus avec le jeu de données Chlamydiae de Caporaso et al. (2011), où la phylogénie se positionne au sein de la région de confiance de l’arbre des corrélations (figure 3.5). Ce jeu de données se caractérise par sa faible taille : seulement \(26\) échantillons et beaucoup de taxons peu abondants ou peu prévalents, ce qui produit une région de confiance très large. De plus, il contient des échantillons provenant de \(8\) environnements très différents (océan, selles, sol…), et ces niches écologiques se retrouvent à la fois dans la phylogénie (Philippot et al., 2010) et dans l’arbre des corrélations.

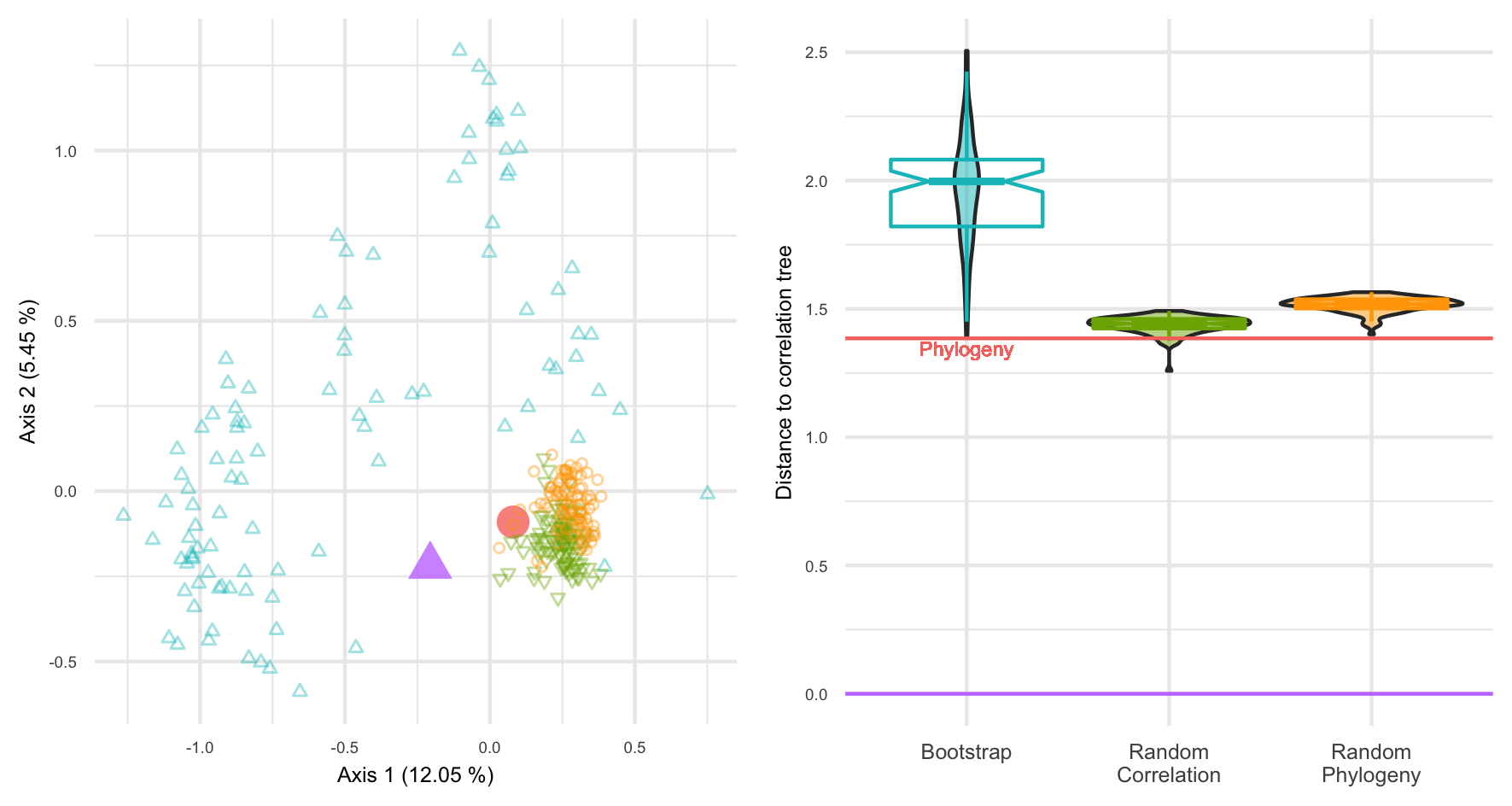
Figure 3.5: Distances BHV au sein de la forêt d’arbres pour le jeu de données Chlamydiae.

À l’aide de ces résultats, nous pouvons affirmer que l’arbre des corrélations ne capte pas le même signal que la taxonomie ou la phylogénie, en particulier lorsque l’on se concentre sur un seul biome. Les taxons avec un profil d’abondance similaire sont regroupés ensemble dans l’arbre des corrélations, par construction, mais pas dans la taxonomie ou la phylogénie, ce qui ne fait d’aucun de ces deux derniers arbres un bon candidat pour trouver des groupes de taxons différentiellement abondants.

Nous obtenons les mêmes conclusions en utilisant la distance RF, comme le montre la figure 3.6.

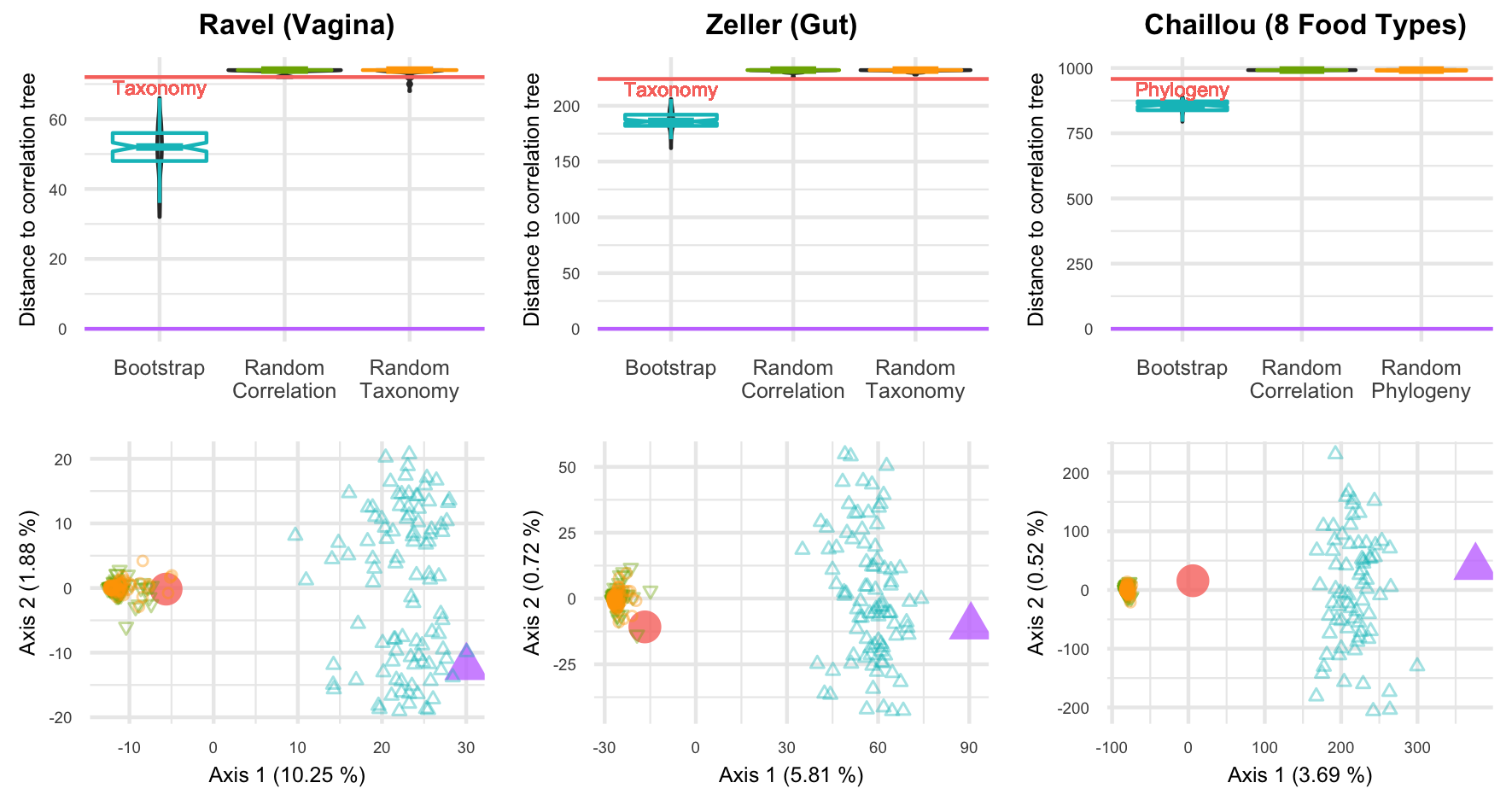
Figure 3.6: Distances RF au sein de la forêt d’arbres pour trois jeux de données.

3.4.3 Choix de l’arbre et lissage de z-score

L’arbre des corrélations étant différent de l’arbre taxonomique, nous avons regardé l’impact du choix de l’arbre sur la procédure TreeFDR (Xiao et al., 2017), à la fois sur des données simulées et sur un jeu de données réel.

Afin de simuler un jeu de données métagénomique, nous avons d’abord appris du jeu de données de Wu et al. (2011) les paramètres d’une loi Dirichlet-multinomiale \(\mathcal{D}(\gamma)\). Nous créons ensuite un jeu de données échantillon par échantillon comme suit : (i) la profondeur de séquençage \(N_i\) est tirée selon une loi binomiale négative de moyenne \(10000\) et de dispersion \(25\), (ii) le vecteur de proportion \(\alpha_i\) est tirée dans une distribution de Dirichlet de paramètre \(\gamma\) puis (iii) les comptages de l’échantillon \(i\) sont tirés dans une loi multinomiale de paramètre \(N_i\) et \(\alpha_i\).

Une fois le jeu de données simulées obtenu, il reste à créer des taxons différentiellement abondants. La procédure est illustrée dans la figure 3.7. Tout d’abord, les échantillons sont aléatoirement assignés à un groupe \(A\) ou \(B\) (quadrant B). Ensuite, les taxons différentiellement abondants sont sélectionnés uniformément dans l’arbre (quadrant C). Enfin, l’abondance de ces taxons au sein du groupe \(B\) est multipliée par un fold-change (quadrant D).

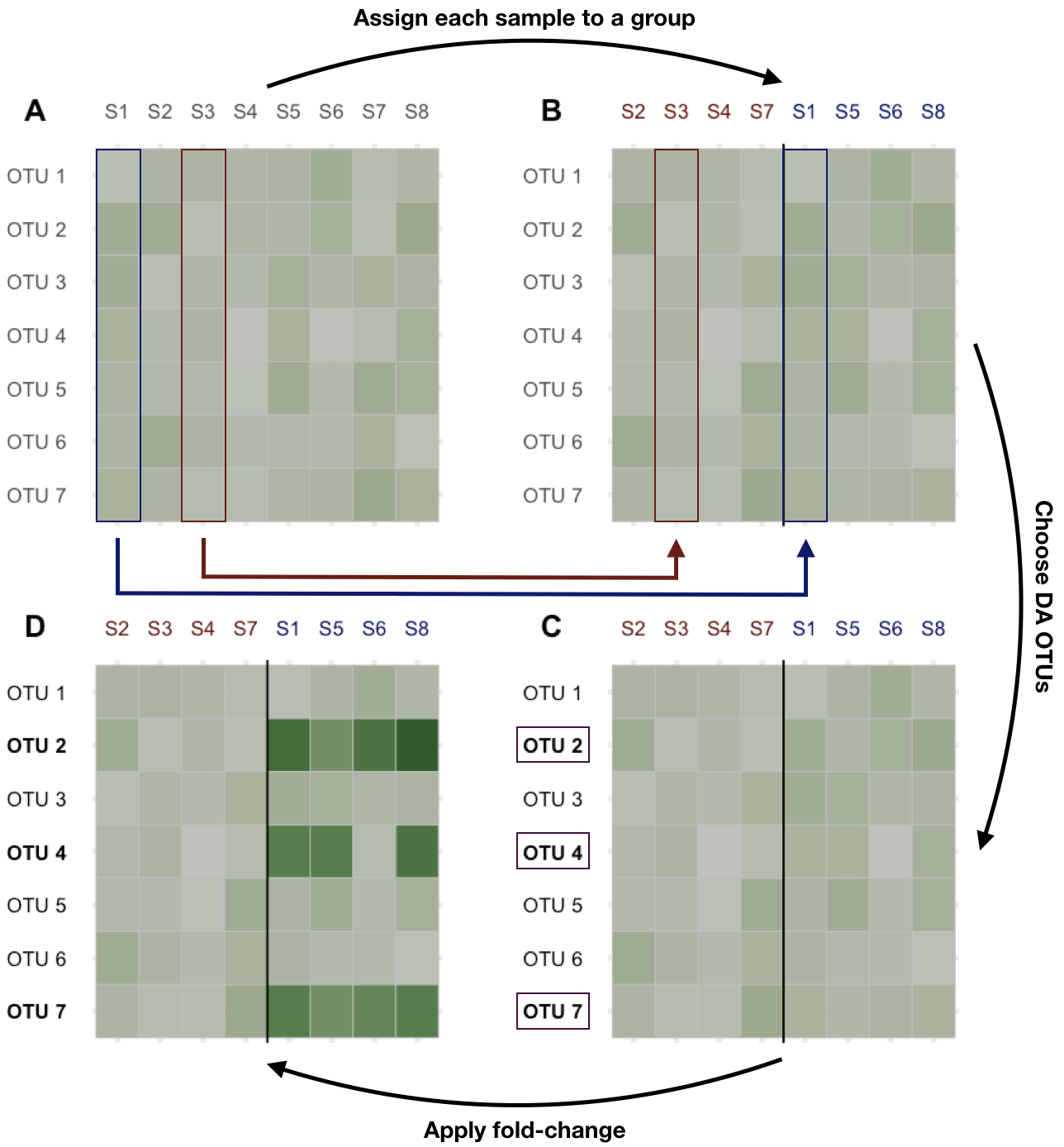
Figure 3.7: Création de taxons différentiellement abondants au sein d’un jeu de données.

On qualifiera ce schéma de simulation de paramétrique.

Il est également possible d’utiliser directement les comptages d’un jeu de données réel homogène, comme celui des individus sains de Brito et al. (2016) –au lieu d’en simuler suivant une Dirichlet-multinomiale– puis d’appliquer la procédure de la figure 3.7 pour générer de l’abondance différentielle. On parlera alors d’un schéma non-paramétrique –par opposition à la simulation paramétrique, précédemment décrite.

Nous avons généré des jeux de données d’abondance différentielle puis évalué la performance des corrections Benjamin-Hochberg et de TreeFDR avec l’arbre des corrélations, la taxonomie, un arbre des corrélations aléatoire et une taxonomie aléatoire.

Regardons dans un premier temps les simulations non paramétriques (issues d’un jeu de données réelles). Tout d’abord, notons que la procédure échoue dans \(4~\%\) des simulations pour l’ensemble des arbres, et jusqu’à \(8~\%\) quand on se limite à l’arbre des corrélations. Notons ensuite que les hyperparamètres \(k\) et \(\rho\) qui contrôlent le niveau de lissage des \(z\)-scores sont assez éloignés de \(1\) (très bas pour \(k\), très haut pour \(\rho\)), ce qui réduit considérablement l’impact du lissage. Les distributions de la figure 3.8 montrent que dans plus de la moitié des simulations, le lissage déplace le \(z\)-score de moins de \(10^{-2}\). Dans le cas où l’arbre utilisé est celui des corrélations, un déplacement des \(z\)-scores d’amplitude supérieure à \(10^{-2}\) ne se produit que dans \(5~\%\) des simulations.

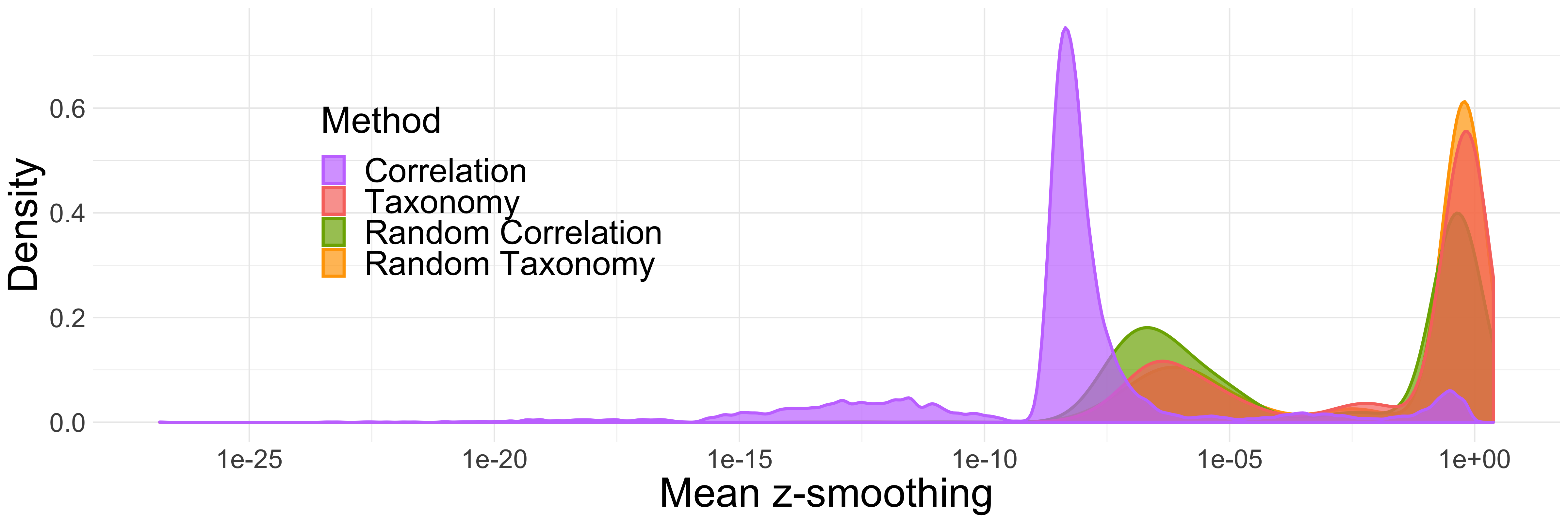
Figure 3.8: Distribution des moyennes des valeurs absolues des différences entres les \(z\)-scores avant et après lissage, pour les simulations non paramétriques.

Au niveau du contrôle du FDR, seul BH contrôle systématiquement le taux de faux positifs en deçà de \(5~\%\) (figure 3.9 bas). Les procédures hiérarchiques peuvent dépasser ce seuil, allant jusqu’à \(7~\%\) lorsque la proportion réelle d’espèces différentiellement abondantes est faible (\(\leq 10~\%\)). Enfin, BH est la méthode qui a le plus important TPR, quelque soit le fold-change ou la proportion d’hypothèses nulles (figure 3.9 haut). Devant ces résultats, nous pouvons affirmer que l’utilisation d’un arbre dans la procédure de lissage de TreeFDR, même adapté aux données d’abondances comme l’arbre des corrélations, ne permet pas d’avoir des procédures plus puissantes que BH.

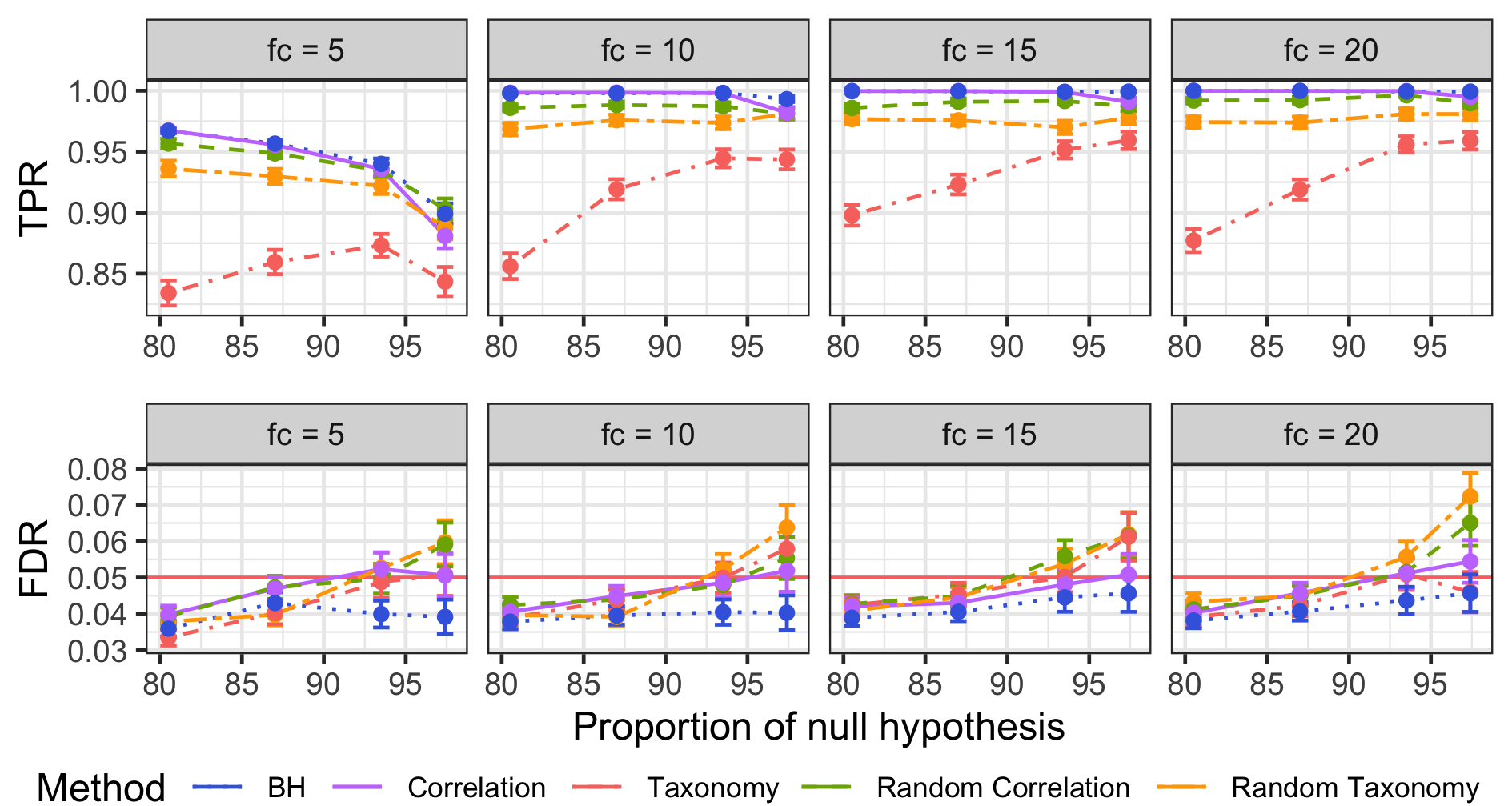
Figure 3.9: Moyennes et écart-types de la moyenne des TPR et FDR pour les simulations non paramétriques avec différents fold-changes et proportions d’hypothèses nulles.

Les simulations paramétriques donnent des résultats semblables aux simulations non-paramétriques, comme le montre la figure 3.10. On note cependant un effondrement du TPR avec ce schéma de simulation.

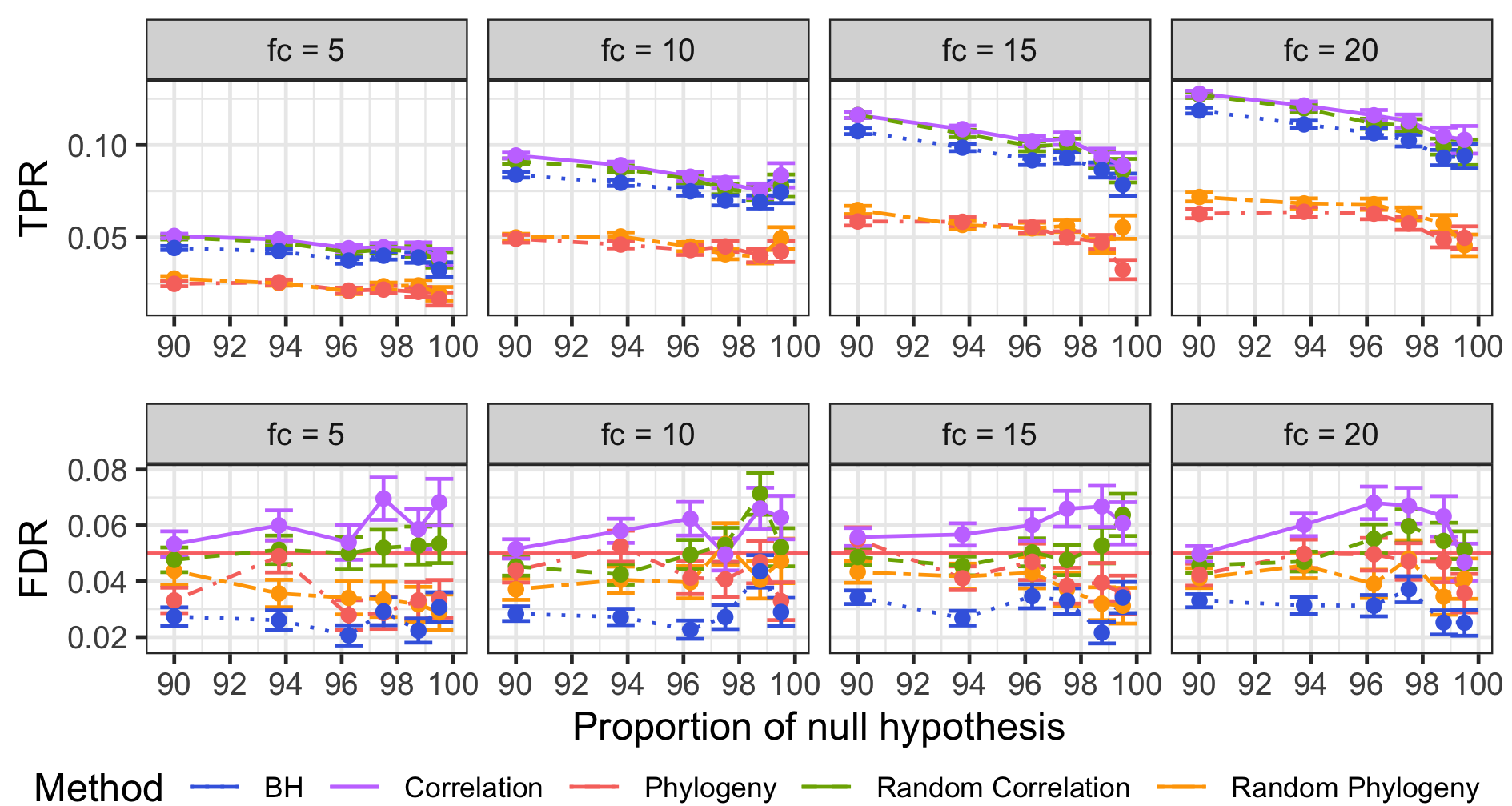
Figure 3.10: Moyennes et écart-types de la moyenne des TPR et FDR pour les simulations paramétriques avec différents fold-changes et proportions d’hypothèses nulles.

Nous avons également testé l’influence de l’arbre sur la procédure de lissage avec le jeu de données de Zeller et al. (2014). Celui-ci a été analysé à deux niveaux de granularité différents : genre et MSP. La figure montre le nombre de genres (à gauche) ou de MSPs (à droite) détectés pour différents seuils jusqu’à \(\alpha = 0.15\).

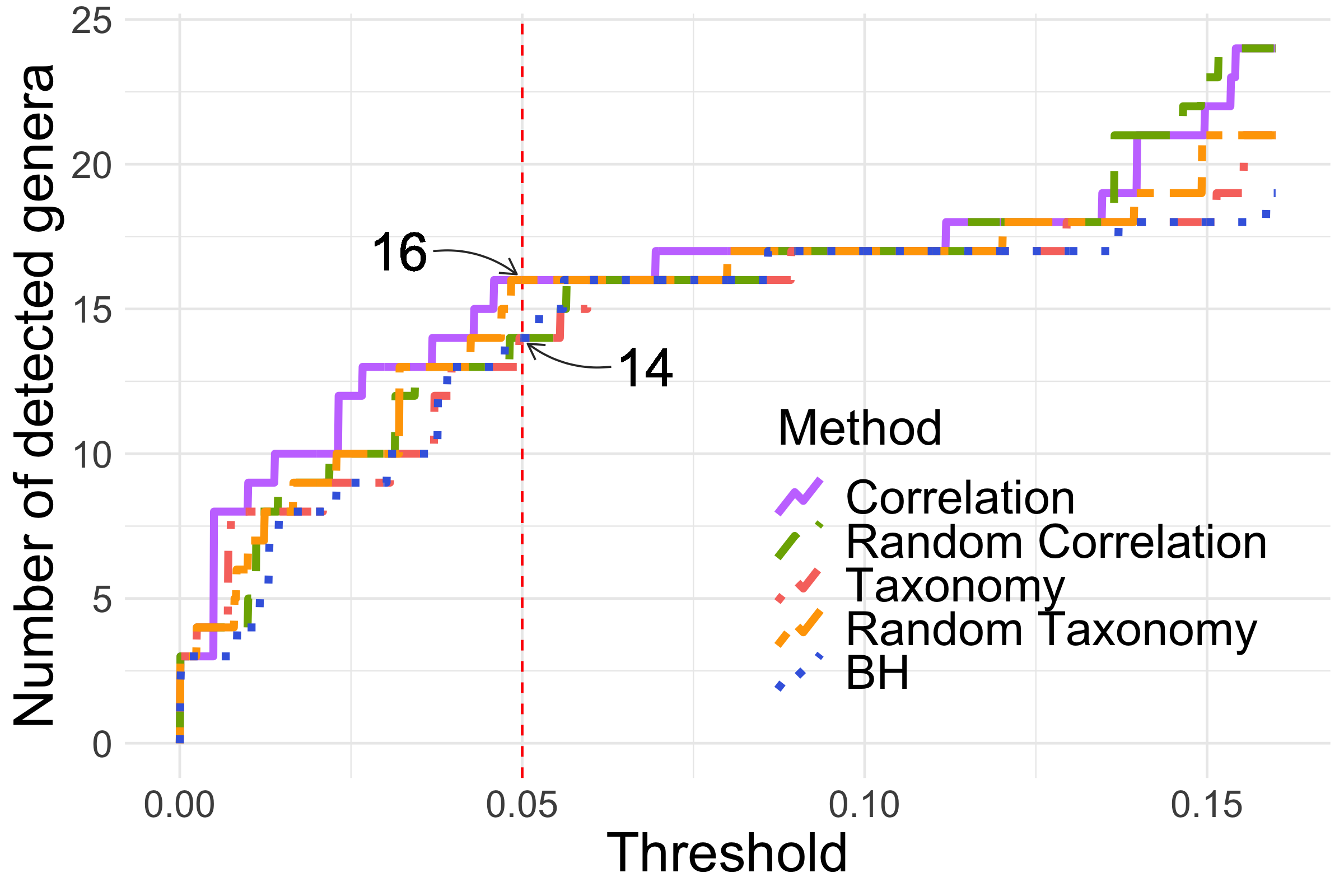
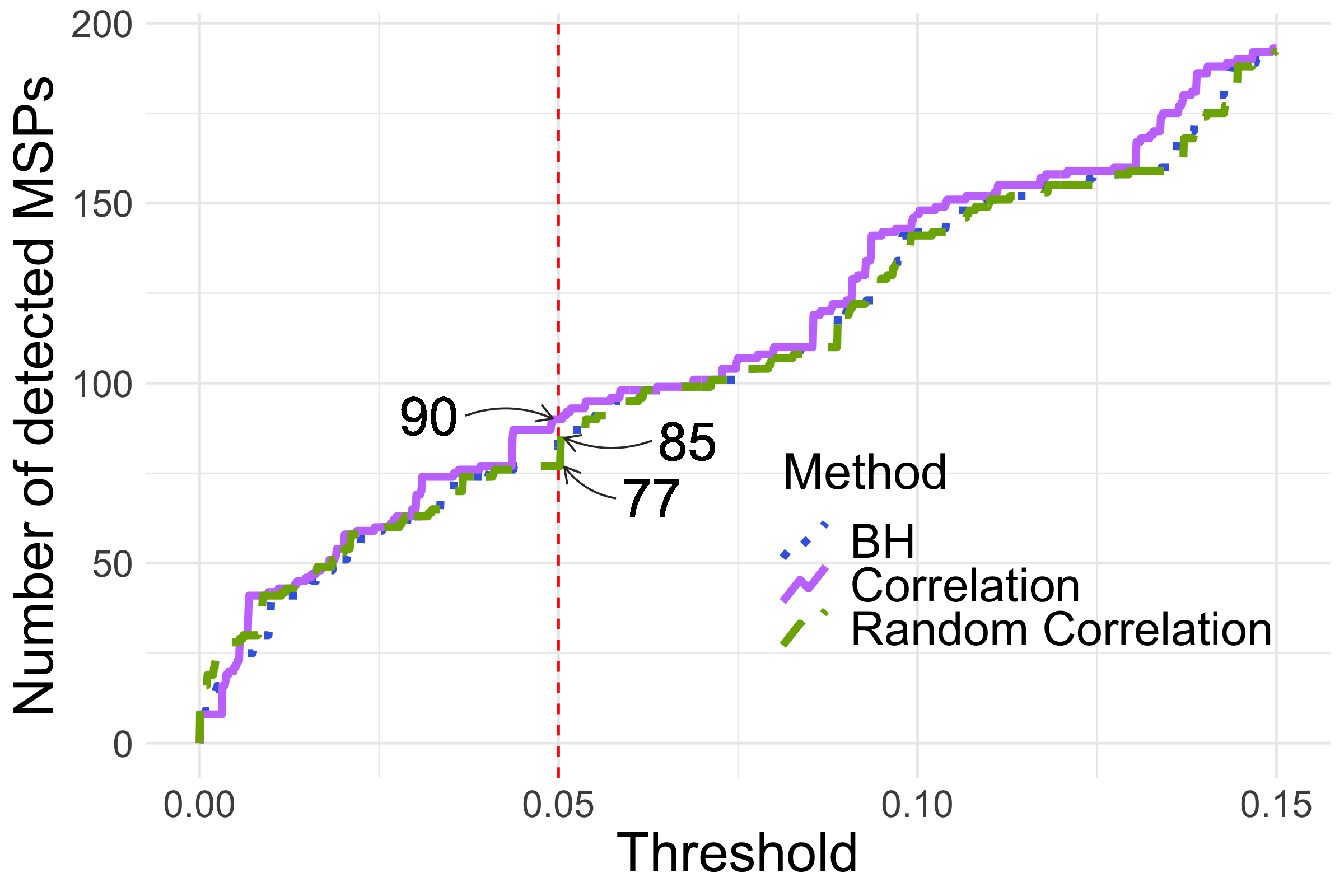
Figure 3.11: Moyennes et écart-types de la moyenne des TPR et FDR pour les simulations non paramétriques avec différents fold-changes et proportions d’hypothèses nulles.

Dans les deux cas, l’arbre des corrélations détecte pour la majorité des seuils plus de taxons que BH mais la différence est très faible, y compris en comparaison avec les arbres aléatoires. Si l’on regarde au niveau des MSPs à \(\alpha = 0.05\), l’arbre des corrélations permet de détecter 5 taxons de plus que la procédure BH classique. Ces taxons ne sont cependant pas regroupés dans des clades différentiellement abondants. Il semblerait alors que cela soit plutôt la correction de permutation post-lissage, qui a pour objectif de contrôler le FDR discret, plutôt que le lissage lui-même qui produise cet effet. Le FDR discret prend en compte des distributions non continues des \(p\)-valeurs sous l’hypothèse nulle et est adapté aux données de comptage. Cette méthode de correction a été déclarée plus performante pour détecter des taxons différentiellement abondants que la procédure BH classique (Jiang et al., 2017).

3.4.4 Choix de l’arbre et FDR hiérarchique

Le fait que le FDR hiérarchique ne permette pas de spécifier a priori un niveau de FDR cible mais uniquement de le calculer a posteriori pour une liste d’espèces différentiellement abondantes le rend inadapté à des simulations comme celles de la section 3.4.3. C’est pourquoi nous ne regarderons l’impact du choix de l’arbre sur cette procédure qu’au travers de jeux de données réelles.

Nous avons d’abord réanalysé le jeu de données Chlamydiae (Sankaran & Holmes, 2014), comme dans l’article original, en utilisant un seuil pour la correction au niveau des familles \(\alpha = 0.1\). Avec la phylogénie, \(8\) OTUs ont été détectés comme différentiellement abondantes et la procédure garantit un FDR a posteriori de \(\alpha'=0.32\). Si l’on utilise l’arbre des corrélations à la place, on trouve \(3\) OTUs supplémentaires pour un FDR a posteriori comparable de \(\alpha'=0.324\). Les boîtes à moustaches des abondances de ces OTUs (figure 3.12 E, F) montrent qu’elles sont bien plus abondantes dans les échantillons de sol que dans les autres biomes, ce qui confirme leur statut d’OTU différentiellement abondante.

La figure 3.12 résume cette analyse en indiquant quelles OTUs sont détectées avec l’une ou l’autre des méthodes et en précisant les évidences brutes (\(\mathfrak{e} = -\log\pv\)) correspondantes aux feuilles des arbres. Intéressons nous plus particulièrement à l’OTU \(547~579\) (marquée d’une étoile rouge) qui a été détectée par l’arbre des corrélations (figure 3.12 D) mais pas par la phylogénie (figure 3.12 A). Elle n’a pas été testée par la phylogénie car elle est entourée d’espèces non différentiellement abondantes qui masquent le signal (figure 3.12 B). À l’inverse, dans l’arbre des corrélations (figure 3.12 D), elle se situe dans un clade où toutes les OTUs sont différentiellement abondantes, ce qui permet à la procédure de rejeter tous les sous-arbres contenant \(547~579\) jusqu’à la feuille correspondant à \(547~579\), sans s’arrêter au niveau des branches internes.

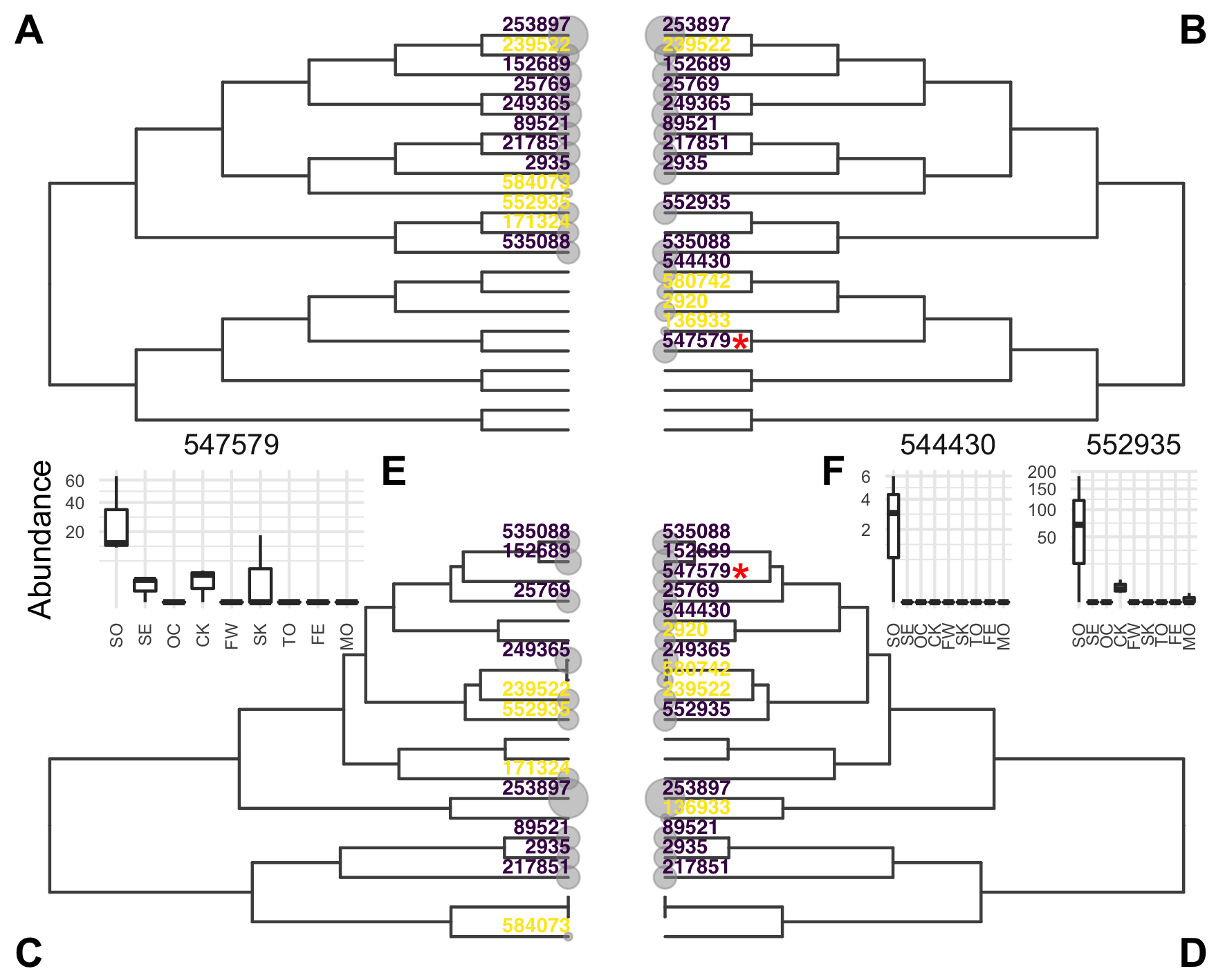
Figure 3.12: Les évidences brutes sont représentées aux feuilles de la phylogénie (A et C) ou de l’arbre des corrélations (B et D). Les OTUs considérées différentiellement abondantes pour la phylogénie (A et B) ou pour l’arbre des corrélations (C et D) sont en violet. Les OTUs testées mais non rejetées sont en jaune.

On peut remarquer que le FDR a posteriori est assez élevé, à \(0.324\). En effectuant une correction par BH à ce même niveau, on détecte \(15\) OTUs différentiellement abondantes, soit quatre de plus que la correction avec l’arbre des corrélations. Ceci peut s’expliquer par le fait que hFDR contrôle le FDR dans le pire des cas tandis que le FDR effectif pourrait être bien plus bas que cette borne pessimiste (Yekutieli, 2008).

Avec cette approche descendante, l’arbre des corrélations est plus adapté que la phylogénie. En regroupant les espèces corrélées et donc potentiellement différentiellement abondantes au sein d’un même sous-arbre, il permet de concentrer les différents signaux dans une portion d’arbre et d’éviter qu’ils ne soient dilués dans tout l’arbre, comme c’est le cas avec la phylogénie.

Nous avons ensuite analysé le jeu de données Chaillou (Chaillou et al., 2015) restreint aux Bacteroidetes. L’utilisation d’un seuil \(\alpha=0.01\) au niveau des familles a conduit à un contrôle du FDR a posteriori à \(\alpha'=0.04\) à la fois pour la phylogénie et l’arbre des corrélations. Le premier arbre a détecté \(28\) OTUs différentiellement abondantes contre \(34\) pour la phylogénie.

En observant l’abondance des \(22\) OTUs détectées simultanément par les deux procédures ou des \(18\) détectées par une seule des deux (figure 3.13), on remarque que chacune d’entre elles (i) est absente ou en dessous du seuil de détection dans au moins un des aliments et (ii) a de fortes prévalences et abondances dans au moins un autre aliment. Ceci valide leur caractère différentiellement abondant et permet de les considérer comme des vrais positifs.

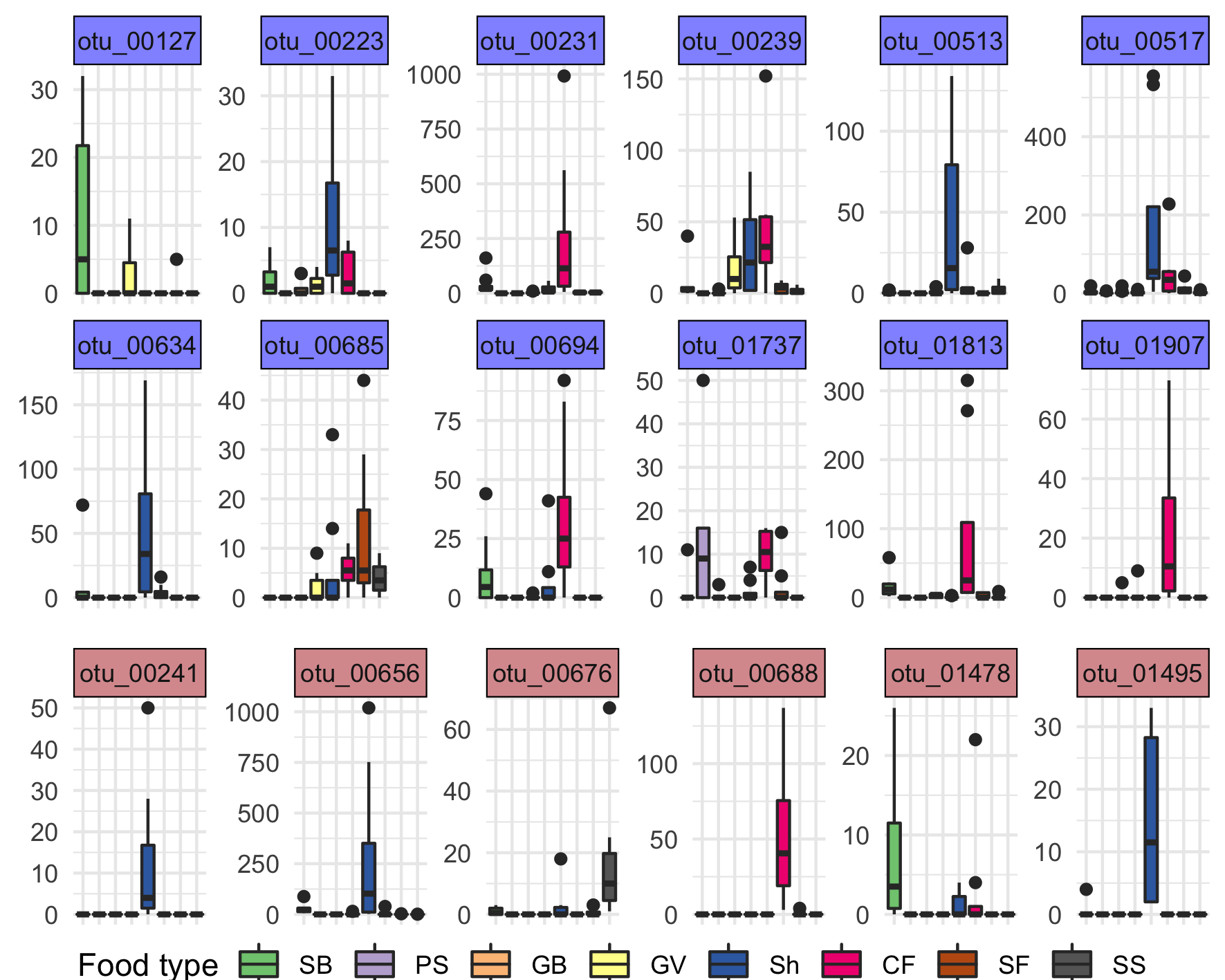
Figure 3.13: Abondances des OTUs détectées uniquement par l’arbre des corrélations (en bleu) ou par la phylogénie (en rouge).

Si l’on regarde les OTUs détectées sur leurs arbres respectifs, comme représentées sur la figure 3.14, les OTUs détectées uniquement par l’arbre des corrélations sont éparpillées dans la phylogénie, de manière similaire à ce qu’on a pu observer pour le jeu de données Chlamydiae. À l’inverse, les OTUs différentiellement abondantes uniquement dans la phylogénie sont proches d’OTUs détectées pour l’arbre des corrélations mais ne sont pas détectées à cause de la faible puissance du test de Fisher, pratiqué par défaut dans StructSSI et peu adapté aux données métagénomiques.

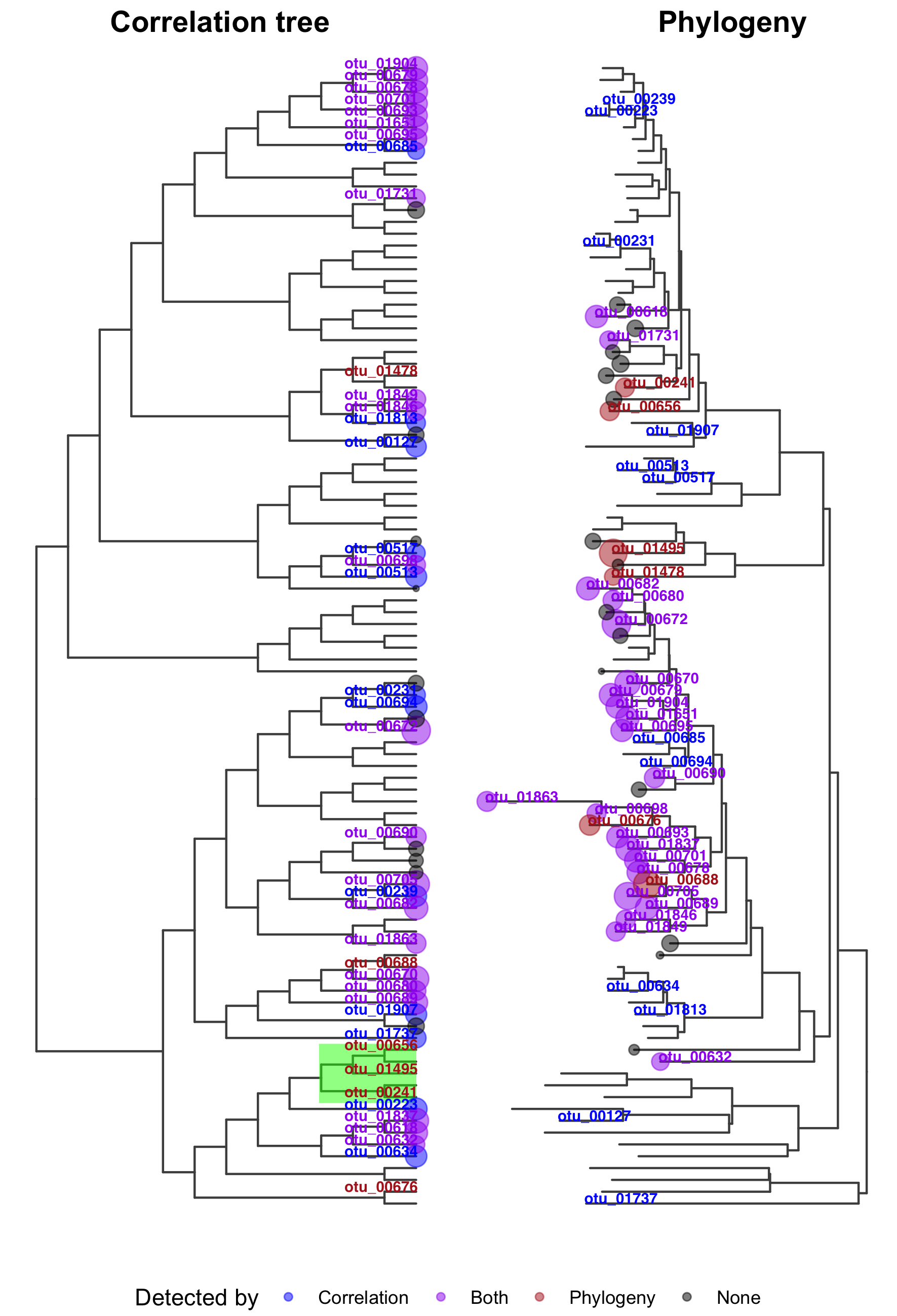
Figure 3.14: Évidences des OTUs détectées avec l’arbre des corrélations (à droite) ou la phylogénie (à gauche).

Si l’on regarde plus attentivement les cinq OTUs du cadre vert de la figure 3.14, on a trois OTUs qui ont été détectées uniquement par la phylogénie et non par l’arbre des corrélations alors qu’elles appartiennent au même clade de cinq individus dans celui-ci. La figure 3.15 met l’accent sur ces cinq OTUs, qui ne sont présentes quasiment que dans les crevettes. Le test de Fisher couplé au bruit causé par l’agrégation des données fait qu’on ne descend pas dans le sous-arbre en question. L’inaptitude de l’arbre des corrélations à identifier ces taxons est donc imputable à l’utilisation d’un test inadapté : remplacer le test de Fisher par un test non paramétrique de Kruskall-Wallis aurait permis à la procédure hiérarchique sur l’arbre des corrélations d’identifier l’ensemble des OTUs du clade.

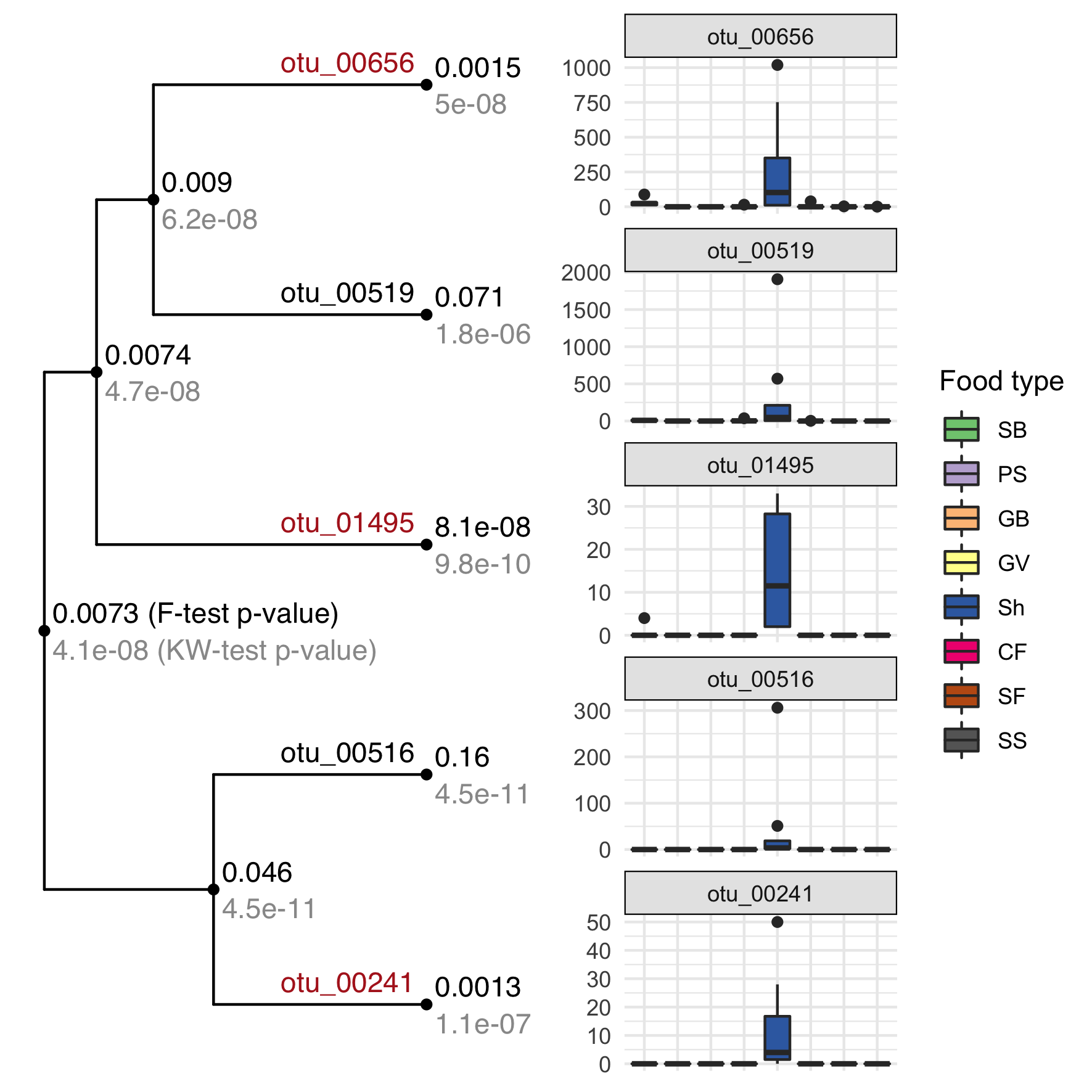
Figure 3.15: Focus sur les cinq OTUs du cadre vert de la figure 3.14.