Available measures

Available measures in evabic

ebc_allmeasures

Format

An object of class character of length 18.

Details

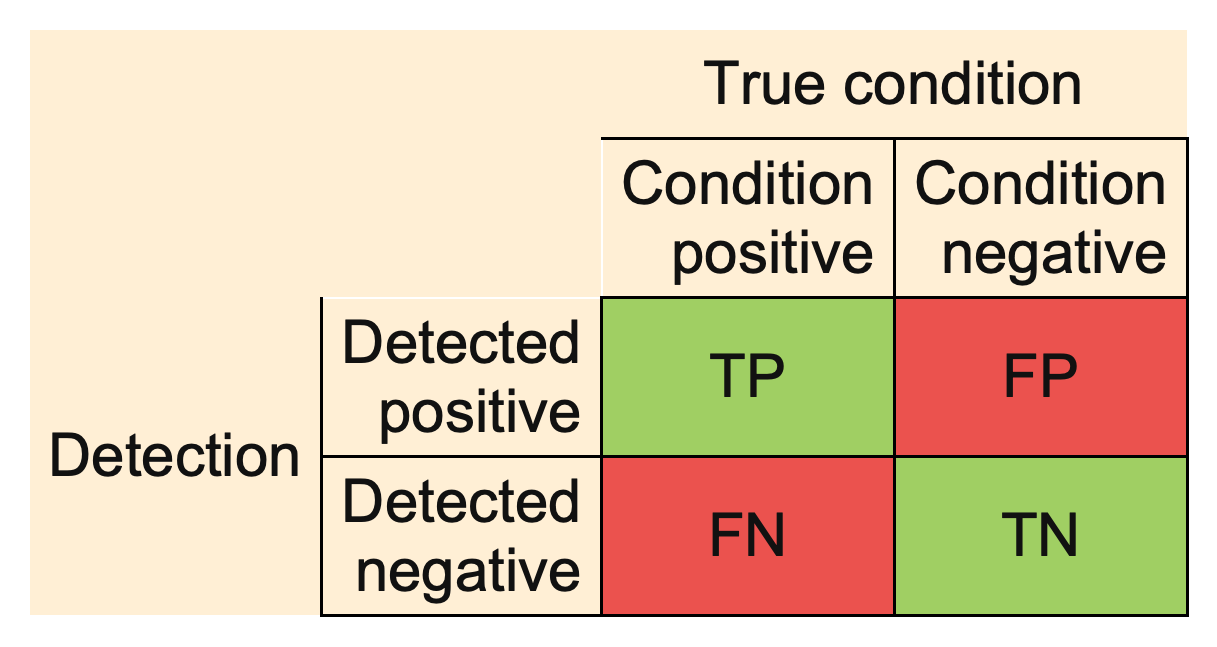
TP

True Positive

FP

False Positive

FN

False Negative

TN

True Negative

TPR

True Positive Rate or Sensitivity or Recall or Power $$TPR = \frac{TP}{TP + FN} = 1 - FNR$$

TNR

True Negative Rate or Specificity $$TNR = \frac{TN}{FP + TN} = 1 - FPR$$

PPV

Positive Predictive Value or Precision $$PPV = \frac{TP}{TP + FP} = 1 - FDR$$

NPV

Negative Predictive Value $$NPV = \frac{TN}{TN + FN} = 1 - FOR$$

FNR

False Negative Rate or Type II Error Rate or Miss Rate $$FNR = \frac{FN}{TP + FN} = 1 - TPR$$

FPR

False Positive Rate or Type I Errors Rate or Fall-out $$FPR = \frac{FP}{FP + TN} = 1 - TNR$$

FDR

False Discovery Rate $$FDR = \frac{FP}{FP + TP} = 1 - PPV$$

FOR

False Omission Rate $$FOR = \frac{FN}{TN + FN} = 1 - NPV$$

ACC

Accuracy $$ACC = \frac{TP + TN}{TP + FP + FN + TN}$$

BACC

Balanced Accuracy $$BACC = \frac{\frac{TP}{TP + FN} + \frac{TN}{FP + TN}}{2}$$

F1

F1 Score $$F1 = \frac{2 TP}{2TP + FP + FN} = \frac{2}{\frac{1}{TPR} + \frac{1}{PPV}}$$

PLR

Positive Likelihood Ratio or LR+ or Likelihood Ratio for Positive Results $$PLR = \frac{TPR}{1 - TNR}$$

NLR

Negative Likelihood Ratio or LR- or Likelihood Ratio for Negative Results $$NLR = \frac{1 - TPR}{TNR}$$

DOR

Diagnostic Odds Ratio $$DOR = \frac{\frac{TP}{FP}}{\frac{FN}{TN}} = \frac{PLR}{NLR}$$

References

https://en.wikipedia.org/wiki/Evaluation_of_binary_classifiers

Examples

ebc_allmeasures
#>  [1] "TP"   "FP"   "FN"   "TN"   "TPR"  "TNR"  "PPV"  "NPV"  "FNR"  "FPR" 
#> [11] "FDR"  "FOR"  "ACC"  "BACC" "F1"   "PLR"  "NLR"  "DOR"